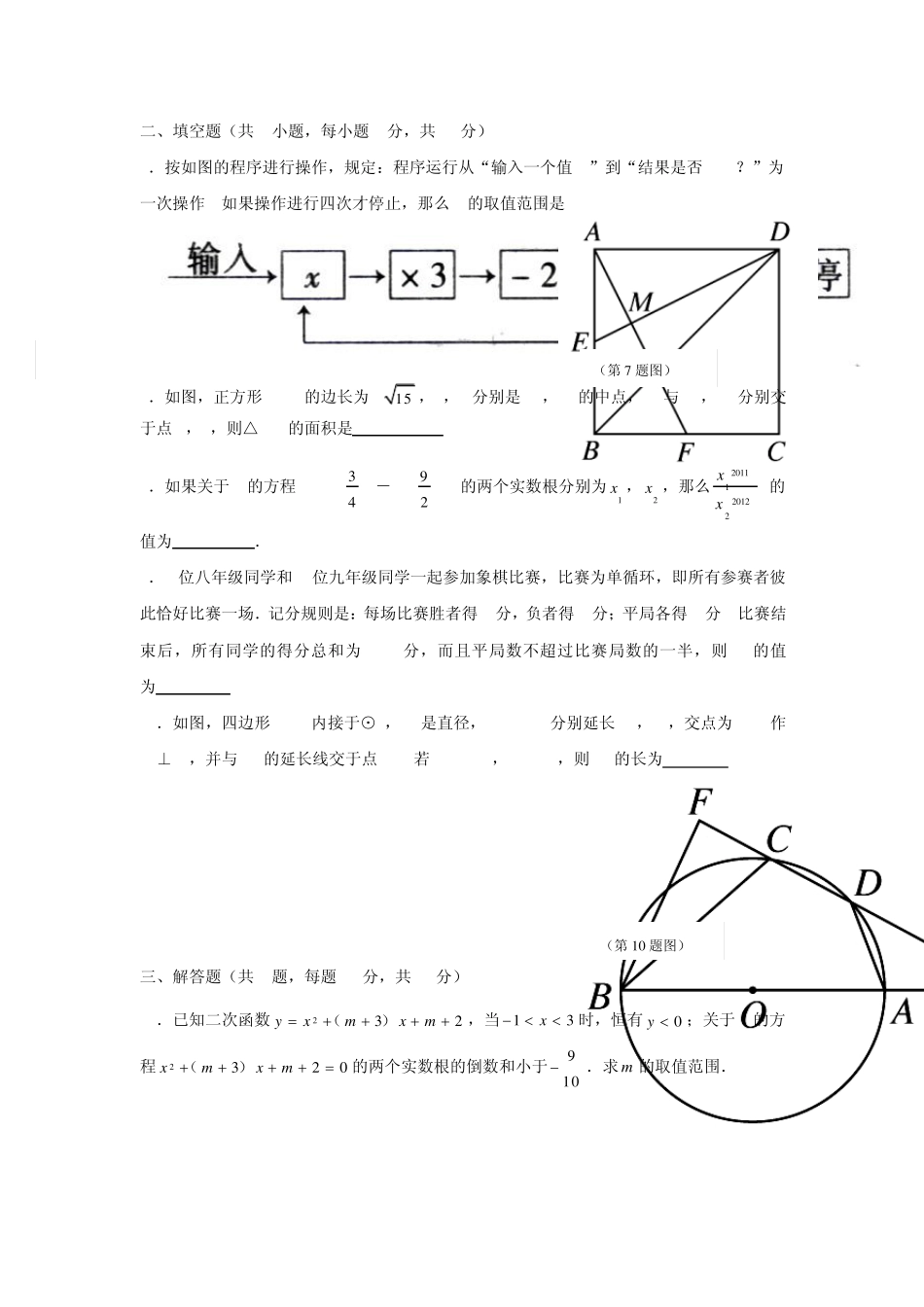
中国教育学会中学数学教学专业委员会2012年 全国初中数学竞赛试题 一、选择题(共5小题,每小题7分,共35分) 1.如果实数a,b,c在数轴上的位置如图所示,那么代数式22||()||aabcabc可以化简为( ). (A)2ca (B)2a2b (C)a (D)a 2.如果正比例函数y = ax(a ≠ 0)与反比例函数y =xb(b ≠0 )的图象有两个交点,其中一个交点的坐标为(-3,-2),那么另一个交点的坐标为( ). (A)(2,3) (B)(3,-2) (C)(-2,3) (D)(3,2) 3.如果ab,为给定的实数,且1ab,那么1121aabab,, ,这四个数据的平均数与中位数之差的绝对值是( ). (A)1 (B)214a (C)12 (D)14 4.小倩和小玲每人都有若干面值为整数元的人民币.小倩对小玲说:“你若给我 2元,我的钱数将是你的n倍”;小玲对小倩说:“你若给我 n元,我的钱数将是你的2倍”,其中n为正整数,则 n的可能值的个数是( ). (A)1 (B)2 (C)3 (D)4 5.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为0123pppp,,,,则0123pppp,,,中最大的是( ). (A)0p (B)1p (C)2p (D)3p (第 1 题图) 二、填空题(共5小题,每小题7分,共35分) 6.按如图的程序进行操作,规定:程序运行从“输入一个值 x”到“结果是否>487?”为一次操作. 如果操作进行四次才停止,那么 x的取值范围是 . 7.如图,正方形 ABCD的边长为 2 1 5 ,E,F分别是 AB,BC的中点,AF与 DE,DB分别交于点 M,N,则△DMN的面积是 . 8.如果关于 x的方程x2+kx+43 k2-3k+92= 0的两个实数根分别为1x ,2x ,那么2 0 1 222 0 1 11xx 的值为 . 9.2位八年级同学和 m位九年级同学一起参加象棋比赛,比赛为单循环,即所有参赛者彼此恰好比赛一场.记分规则是:每场比赛胜者得 3分,负者得 0分;平局各得 1分. 比赛结束后,所有同学的得分总和为 130分,而且平局数不超过比赛局数的一半,则 m的值为 . 10.如图,四边形 ABCD内接于⊙O,AB是直径,AD = DC. 分别延长 BA,CD,交点为 E. 作BF⊥EC,并与 EC的延长线交于点 F. 若 AE = AO,BC = 6,则 CF的长为 . 三、解答题(共4题,每题20分,共80分) 11.已知二次函数232yxmxm(),...