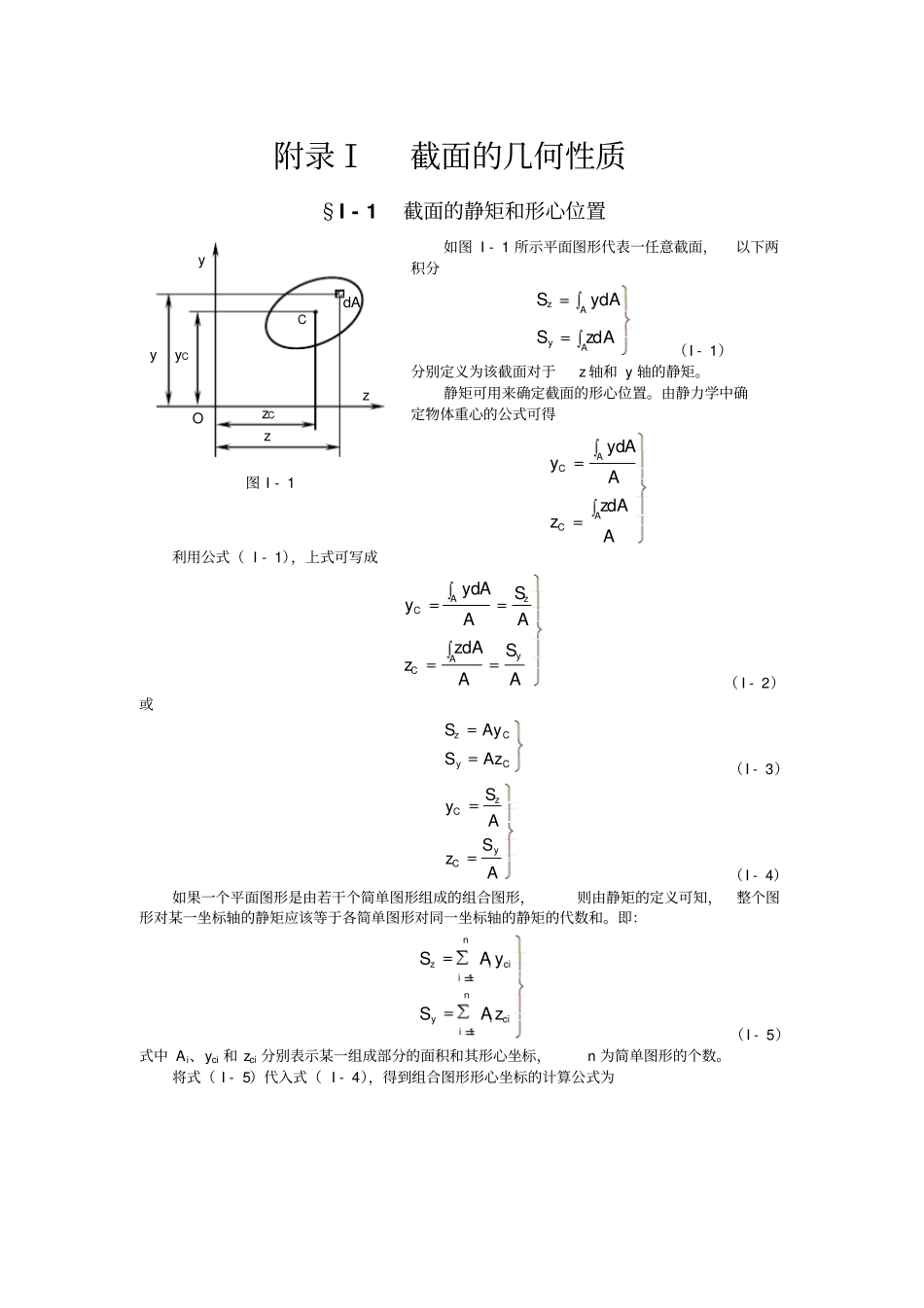
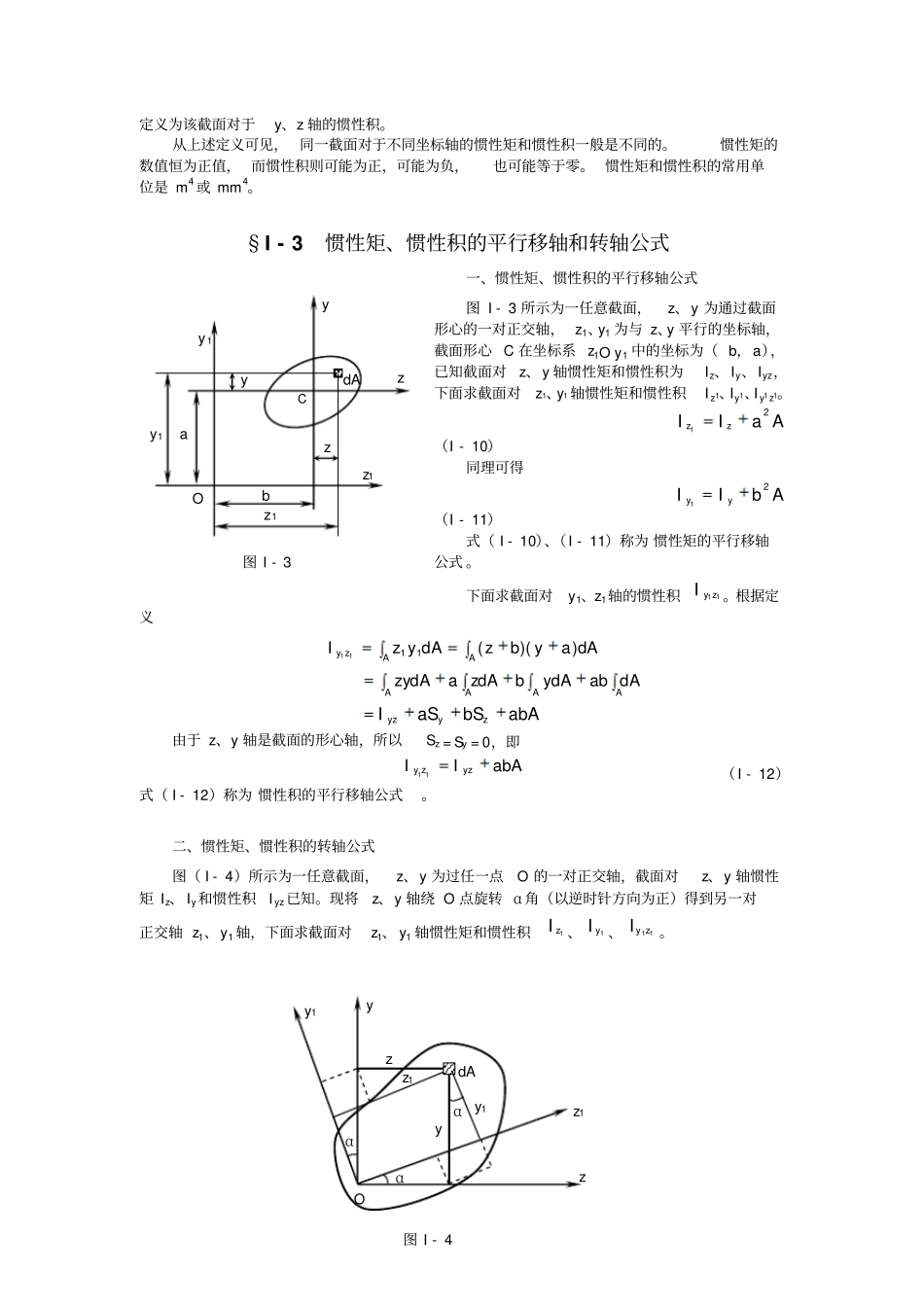
附录Ⅰ截面的几何性质§I - 1截面的静矩和形心位置如图 I - 1 所示平面图形代表一任意截面,以下两积分AzSAySAyAzdd(I - 1)分别定义为该截面对于z 轴和 y 轴的静矩。静矩可用来确定截面的形心位置。由静力学中确定物体重心的公式可得AAzzAAyyACACdd利用公式( I - 1),上式可写成ASAAzzASAAyyyACzACdd( I - 2)或CyCzAzSAyS(I - 3)ASzASyyCzC(I - 4)如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对同一坐标轴的静矩的代数和。即:niciiyniciizzASyAS11(I - 5)式中 Ai、yci 和 zci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。将式( I - 5)代入式( I - 4),得到组合图形形心坐标的计算公式为dA C z y y yC zC O 图 I - 1 zniiniciicniiniciicAzAzAyAy1111( I - 6)例题 I - 1 图 a 所示为对称T 型截面,求该截面的形心位置。解: 建立直角坐标系zOy,其中y 为截面的对称轴。因图形相对于y轴对称,其形心一定在该对称轴上,因此 zC = 0,只需计算yC 值。将截面分成Ⅰ、Ⅱ两个矩形,则AⅠ=0.072m2,AⅡ=0.08m2yⅠ=0.46m,yⅡ=0.2mm323.008.0072.02.008.046.0072.0IIIIIIIII11AAyAyAAyAyniiniciic§I - 2惯性矩、惯性积和极惯性矩如图 I - 2 所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy。现在图形内取微面积dA,dA 的形心在坐标系zOy 中的坐标为y 和 z,到坐标原点的距离为ρ。现定义 y2dA 和 z2dA 为微面积 dA 对 z 轴和 y 轴的 惯性矩 ,ρ2dA 为微面积 dA 对坐标原点的 极惯性矩 ,而以下三个积分AρIAzIAyIAAyAzddd2P22(I - 7)分别定义为该截面对于z 轴和 y 轴的惯性矩以及对坐标原点的极惯性矩。由图( I - 2)可见,222zy,所以有AyzAIIAzyAρI)d(d222P(I - 8)即任意截面对一点的极惯性矩,等于截面对以该点为原点的两任意正交坐标轴的惯性矩之和。另外, 微面积 dA 与它到两轴距离的乘积zydA 称为微面积dA 对 y、z 轴的 惯性积 ,而积分AzydIAyz(I - 9)yC0.12m 0.4m yⅡy Ⅰ0.6m 0.2m OyzⅠⅡCⅠⅠCⅡC例题 I - 1 图dA ρy y O 图 I - 2 zz定义为该截面对于y、z 轴的惯性积。从上述定义可见, 同一截面对于不同坐标轴的惯性矩和惯性积一般是不同的。惯性矩的数值恒为正值...