抛物线的焦点弦_经典性质及其证明过程VIP免费

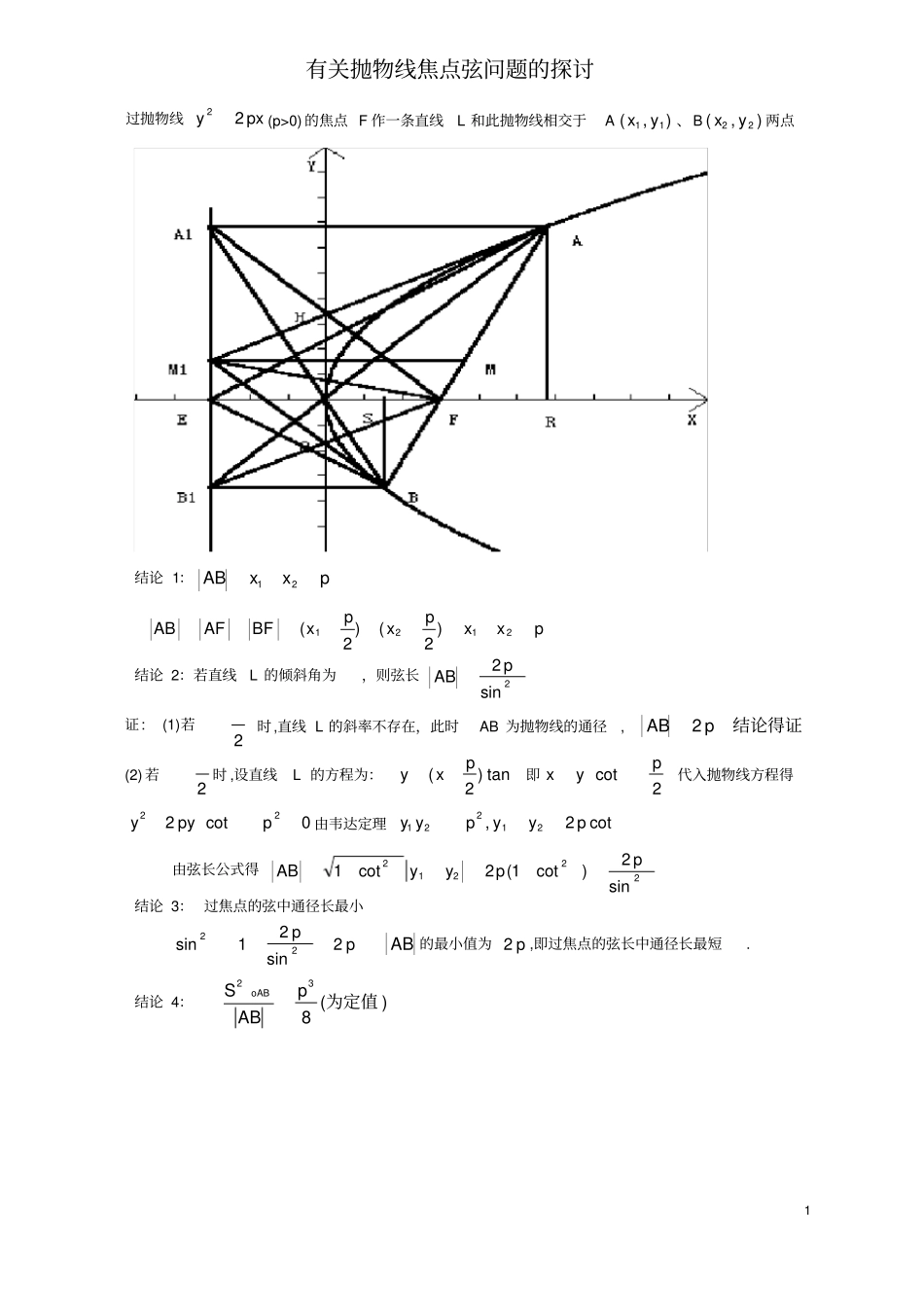
1 有关抛物线焦点弦问题的探讨过抛物线pxy22(p>0) 的焦点 F 作一条直线L 和此抛物线相交于A),(11 yx、B),(22 yx两点结论 1：pxxAB21pxxpxpxBFAFAB2121)2()2(结论 2：若直线L 的倾斜角为，则弦长2sin2pAB证: (1)若2时,直线 L 的斜率不存在，此时AB 为抛物线的通径,结论得证pAB2(2) 若2时 ,设直线L 的方程为：tan)2(pxy即2cotpyx代入抛物线方程得0cot222ppyy由韦达定理cot2,21221pyypyy由弦长公式得22212sin2)cot1(2cot1ppyyAB结论 3： 过焦点的弦中通径长最小pp2sin21sin22AB 的最小值为p2,即过焦点的弦长中通径长最短. 结论 4：)(832为定值pABSoAB2 8sin2sinsin2221sin21sin21sin21sin2132220PABSpppABOFBFAFOFAFOFBFOFSSSOABAFOBFOAB结论 5： (1) 221pyy(2) x 1x 2=42p证44)(,2,22222121222211PPyyxxpyxpyx结论 6：以 AB 为直径的圆与抛物线的准线相切证：设 M 为 AB 的中点，过A 点作准线的垂线AA 1， 过 B 点作准线的垂线BB 1，过 M 点作准线的垂线MM 1，由梯形的中位线性质和抛物线的定义知222111ABBFAFBBAAMM故结论得证结论 7：连接 A 1F、B 1 F 则 A 1FB1F FAAFOAFOAFAAOFAAAFAFAAAFAA11111111//,同理901111FBAFBBFOBA 1FB 1 F 结论 8：（1）AM 1BM 1 （2）M 1FAB （3）BFAFFM21（4）设 AM 1 与 A 1F 相交于 H ，M 1B 与 FB 1相交于 Q 则 M 1， Q，F ，H 四点共圆（5）2121214MMBMAM证：由结论（ 6）知 M 1 在以 AB 为直径的圆上AM 1BM 111FBA为直角三角形，M 1 是斜边 A 1 B 1 的中点111111111AFAFAAFAMFAMFMMA9011111MAAMFAFAA90111FMAAFAM 1FAB BFAFFM21AM 1BM 1 FBFA90111又BAM90FBA11所以 M 1，Q，F,H 四点共圆，22121ABBMAM2121211242MMMMBBAABFAF结论 9： （1）、A O 、B 1 三点共线（ 2）B，O，A 1 三点共线（3）设直线 AO 与抛物线的准线的交点为B1，则 BB 1 平行于 X 轴（4）设直线 BO 与抛物线的准线的交点为A 1，则 AA 1平行于 X 轴3 证：因为pypykyppyyxykoBoA2212111122,221，而221pyy所以122222oBoAkpyyppk所以三点共线。同理可征（2）（3）（4）结论 10：pFBFA211证：过A 点作 AR 垂直 X 轴于点R，过 B 点作 BS 垂直 X 轴于点S，设准线与 x 轴交点为E,的倾斜角为因为直线 L则cos1cosPAFAFAFPFREFERPAFcos11同理可得PBFcos11pFBFA211结论 11：证:AABBEAEBAAFABBBFFABFE...