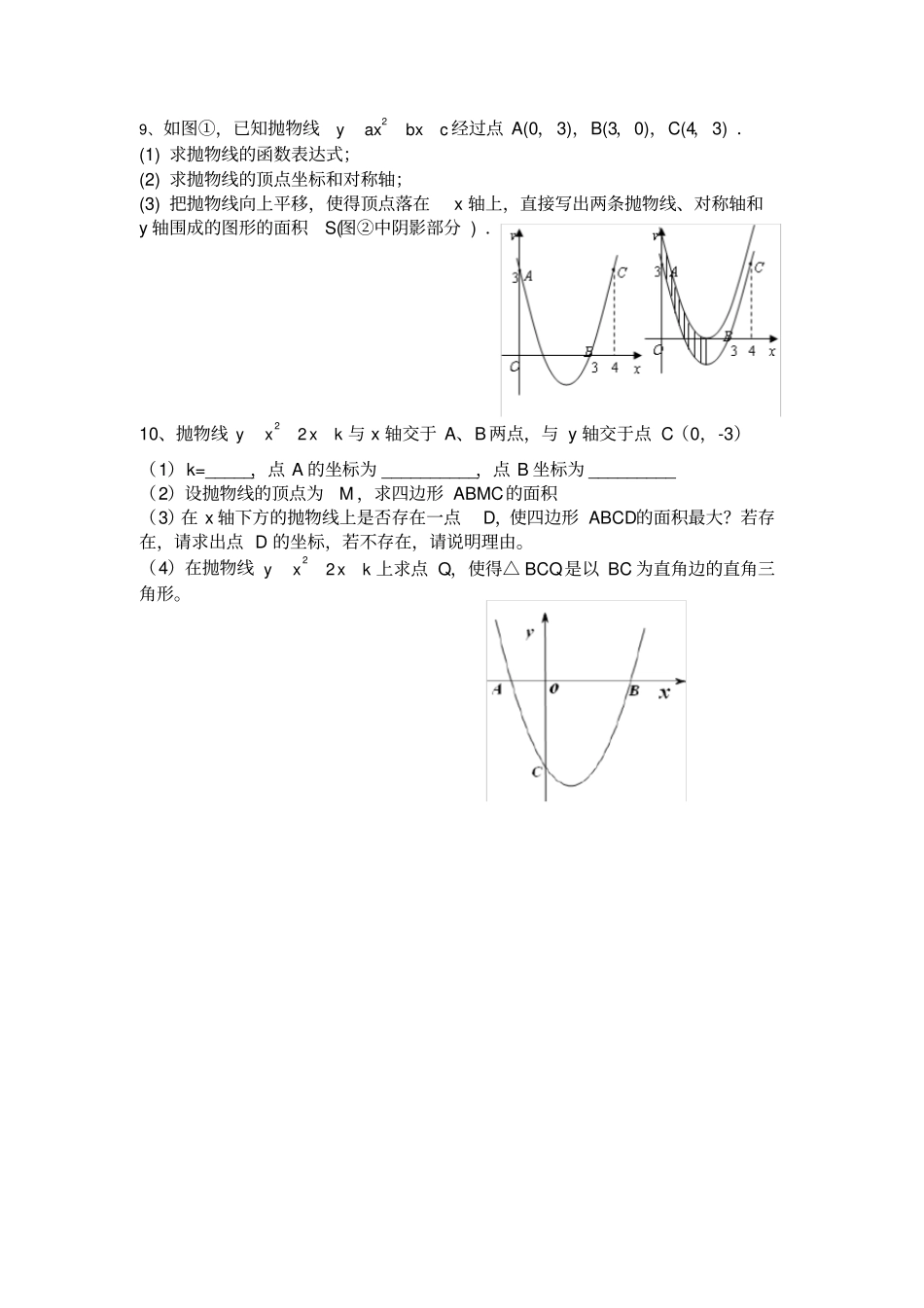
抛物线的面积专题1、如图:抛物线 y=x2-2x-4 与直线 y=x 交于 A、B 两点,点 M 为抛物线的顶点,求△ OBM 的面积变式:若 M 在抛物线对称轴的右侧(且在AB 的下方),当△ OBM 的面积为 10时,求点 M 的坐标2、已知抛物线213y222xx与 x 轴交于 A、B 两点,与 y 轴交于点 C,点 D 为第四象限的抛物线上一点,CD交 x 轴于点 E,若 S△ ACE=S△ DBE,求直线 CD的解析式3、变式 1、若抛物线 y=x2-2x-3 交 x 轴于 A、B 两点,交 y 轴于点 C,M 为顶点,点 N 在 x 轴上。若 S△ BCN=S△BCM 求点 N 的坐标。4 变式 2、如图,抛物线212yxc 与 x 轴交于 A、B,且经过点 D9(3,)2。若点 C 为抛物线上一点,且直线AC把四边形 ABCD分成面积相等的两部分,求直线 AC的解析式5、如图,在平面直角坐标系中, 抛物线21y2x 经过平移得到抛物线2122yxx ,其对称轴与两段抛物线弧所围成的阴影部分的面积为0yx6、如图,在平面直角坐标系xoy 中,△ ABC是等腰直角三角形,∠ BAC=90° ,A(1,0),B(0,2),抛物线2122yxbx的图象过 C点。(1) 求抛物线的解析式(2) 平移抛物线的对称轴所在的直线l,当 l 移动到何处时,恰好将△ ABC的面积分为相等的两部分?(3) 点 P 是抛物线上一动点,是否存在点P,使四边形 PACB是平行四边形?若存在,求出 P 点的坐标,若不存在说明理由。7、如图,抛物线223yxx与 x 轴交于 A、B 两点,点 G(2,y)是抛物线上一点,点 P 是直线 AG 下方的抛物线上一动点,当△APG的面积最大时,求点P的坐标。8、如图,抛物线233384yxx与 x 轴交于 A、B 两点,(点 A 在点 B 的左侧),与 y 轴交于点 C(1)求点 A、B 的坐标(2)设 D 为已知抛物线的对称轴上的任意一点,当△ABD 的面积等于△ ACB的面积时,求点 D 的坐标。(3)设 E 为已知抛物线的对称轴上的任意一点,当△ACE的面积等于△ ACB的面积时,求点 D 的坐标。9、如图①,已知抛物线2yaxbxc 经过点 A(0,3),B(3,0),C(4,3) .(1) 求抛物线的函数表达式;(2) 求抛物线的顶点坐标和对称轴;(3) 把抛物线向上平移,使得顶点落在x 轴上,直接写出两条抛物线、对称轴和y 轴围成的图形的面积S(图②中阴影部分 ) .10、抛物线2y2xxk 与 x 轴交于 A、B 两点,与 y 轴交于点 C(0,-3)(1)k=_____,点 A 的坐标为 __________,点 B 坐标为...