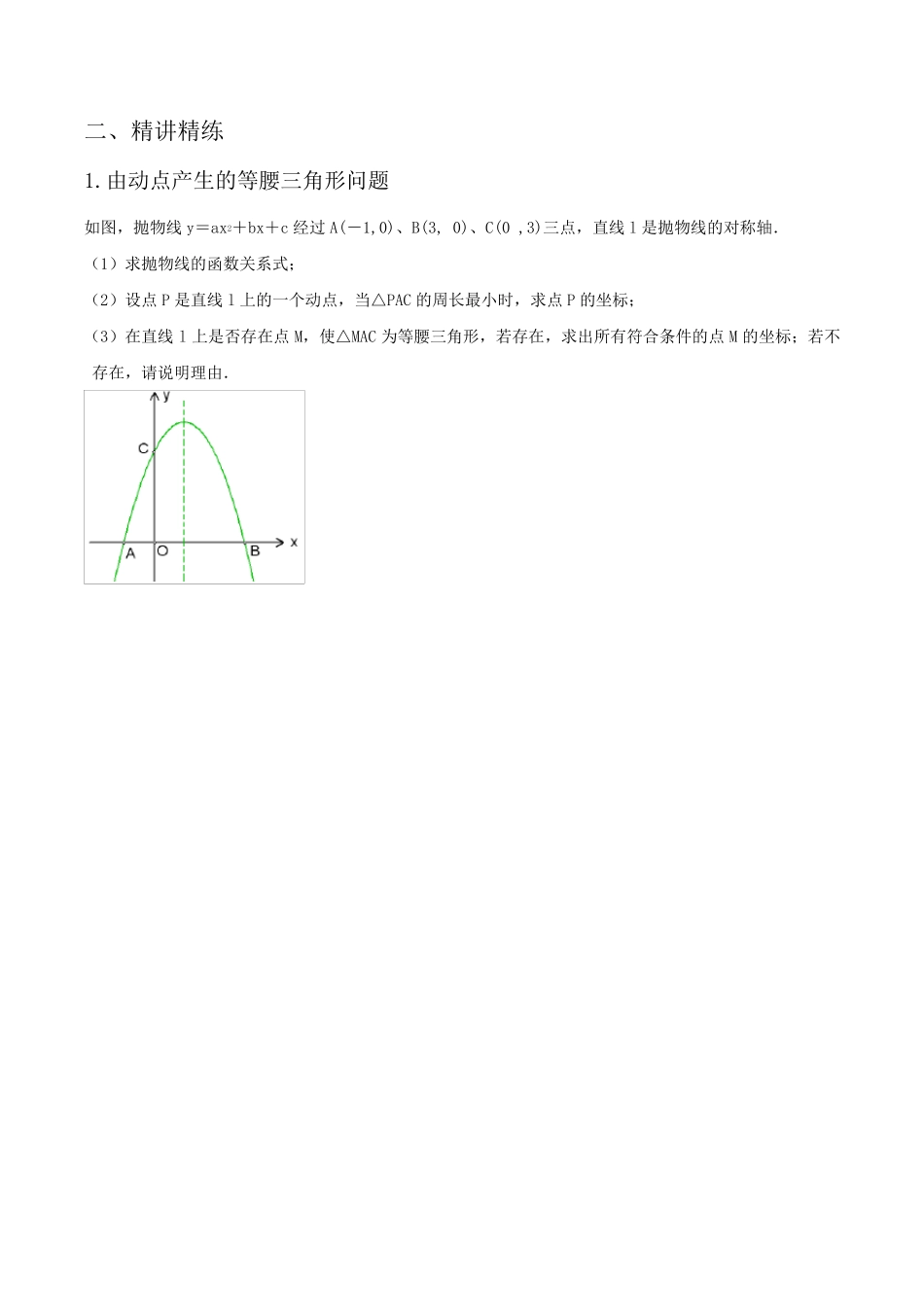
_ Q _ G _ P_ O 二 次 函 数 中 的 动 点 问 题 三 角 形 的 存 在 性 问 题 一 、技巧提炼 1、利用待定系数法求抛物线解析式的常用形式 (1)、【一般式】已知抛物线上任意三点时,通常设解析式为 ,然后解三元方程组求解; (2)、【顶点式】已知抛物线的顶点坐标和抛物线上另一点时,通常设解析式为 求解; 2、二次函数y=ax2+bx+c 与x 轴是否有交点,可以用方程ax2+bx+c = 0 是否有根的情况进行判定; 判别式acb42 二次函数与x 轴的交点情况 一元二次方程根的情况 △ > 0 与x 轴 交点 方程有 的实数根 △ < 0 与x 轴 交点 实数根 △ = 0 与x 轴 交点 方程有 的实数根 3、抛物线上有两个点为A(x1,y),B(x2,y) (1)对称轴是直线2x21xx (2)两点之间距离公式: 已知两点 2211y,xQ,y,xP, 则由勾股定理可得:221221)()(yyxxPQ 练一练:已知A(0,5)和B(-2,3),则AB= 。 4、 常见考察形式 1)已知A(1,0),B(0,2),请在下面的平面直角坐标系 坐标轴上找一点C,使△ABC 是等腰三角形; 总结:两圆一线 方法规律:平面直角坐标系中已知一条线段,构造等腰三角形,用的是“两圆一线”:分别以线段的两个端点为圆心,线段长度为半径作圆,再作线段的垂直平分线; 2)已知A(-2,0),B(1,3),请在平面直角坐标系中坐标轴 上找一点C,使△ABC 是直角三角形; 总结: 两线一圆 方 法 规 律 {平面直角坐标系中已知一条线段,构造直角三角形,用的是“两线一圆”:分别过已知线段的两个端点作已知线段的垂线,再以已知线段为直径作圆; 5、求三角形的面积: (1)直接用面积公式计算;(2)割补法;(3)铅垂高法; 如图,过△ABC 的三个顶点分别作出与水平线垂直的三条直线, 外侧两条直线之间的距离叫△ABC 的“水平宽”(a),中间的 这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高”(h). 我们可得出一种计算三角形面积的新方法: S△ABC=12ah,即三角形面积等于水平宽与铅垂高乘积的一半。 6、二次函数中三角形的存在性问题 解题思路:(1)先分类,罗列线段的长度;(2)再画图;(3)后计算 B C 铅垂高 水平宽 h a A 二、精讲精练 1.由动点产生的等腰三角形问题 如图,抛物线y=ax2+bx+c 经过A(-1,0)、B(3, 0)、C(0 ,3)三点,直线l 是抛物线的对称轴. (1)求抛物...