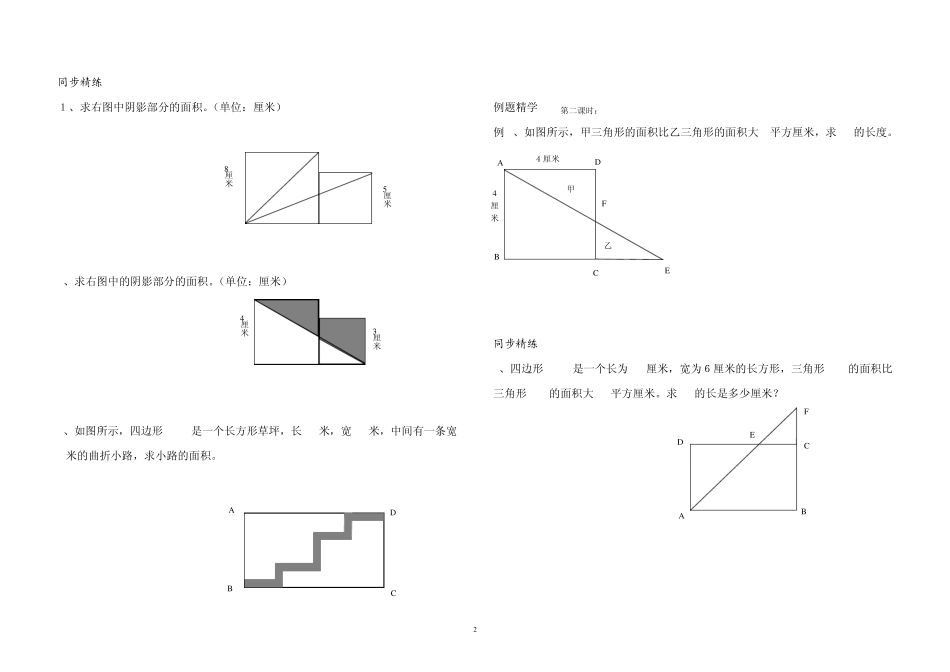
1 第一讲 多边形的面积(一) 知识概述 在数学课上我们已经掌握了几种基本图形的面积计算公式: 正方形的面积=( ); 长方形的面积=( ); 平行四边形的面积=( ); 三角形的面积=( ); 梯形的面积=( ); 由两个或多个简单的基本几何图形可以组合成一个组合图形,要计算一个组合图形的面积,就要根据图形的基本关系,运用分解、组合、平移、旋转、割补、加辅助线等几种方法来思考。 例题精学:第一课时 例1、已知一个平行四边形的面积是 28平方厘米,求阴影部分的面积。 同步精练 1、下图的梯形中,阴影部分的面积是 150平方厘米,求梯形的面积。 2、已知平行四边形的面积是 48平方厘米,求阴影部分的面积。 3、如果用铁丝围成如下一样的平行四边形,需要用铁丝多少厘米?(单位:厘米) | 12 | 例2、下图中甲和乙都是正方形,求阴影部分的面积。(单位:厘米) 5cm 4cm 15 厘米 25 厘米 5 厘米 6厘米 9 6 6 4 甲 乙 2 同步精练 1、求右图中阴影部分的面积。(单位:厘米) 2、求右图中的阴影部分的面积。(单位:厘米) 3、如图所示,四边形 ABCD是一个长方形草坪,长 20米,宽 14米,中间有一条宽2米的曲折小路,求小路的面积。 例题精学 第二课时: 例 3、如图所示,甲三角形的面积比乙三角形的面积大 6平方厘米,求 CE的长度。 同步精练 1、四边形 ABCD是一个长为 10厘米,宽为6厘米的长方形,三角形 ADE的面积比三角形 CEF的面积大 10平方厘米。求 CF的长是多少厘米? 4厘米 3厘米 D C A B 8厘米 5厘米 甲 A 乙 C B E D F 4 厘米 4厘米 F E A D C B 3 2、平行四边形 ABCD的边长 BC=10厘米,直角三角形 BCE的直角边 EC长为 8厘米,已知阴影部分三角形 ABG和三角形 CDF的面积和比三角形 EFG的面积大 10平方厘米。求 CF的长。 3、正方形 ABCD的边长是 12厘米,已知 DE是 EC长度的2倍,求: (1)三角形 DEF的面积; (2)CF的长。 例 4、两条对角线把梯形 ABCD分割成四个三角形。已知两个三角形的面积如图所示,求另两个三角形的面积各是多少?(单位:厘米) 同步精练 1、如下图,图中 BO=2DO,阴影部分三角形 BCO的面积是 4平方厘米,求梯形的面积是多少平方厘米? 2、下图的梯形 ABCD中,下底是上底的 2倍,E是 AB的中点,求梯形 ABCD的面积是三角形 EDB面积的多少倍? 3、下图梯形 ABCD...