2025年线性代数期末考试试题VIP免费

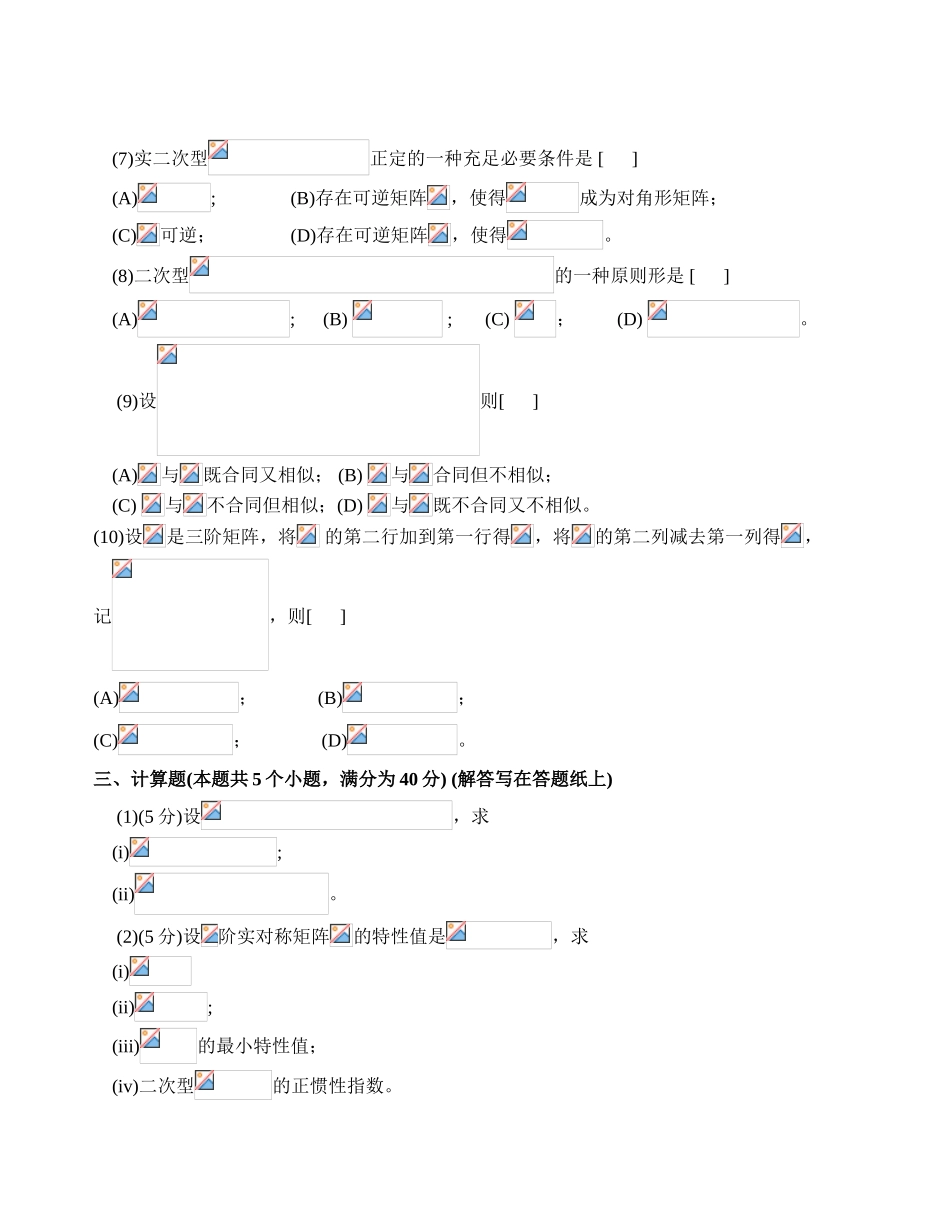
线性代数期末试题 学院 系 姓名 学号 分数 22/12/ 请注意全部答案和解答写在空白答题纸上，标明大题号和小题号。一二三四总分一、填空题（本题共 10 个小题,每小题 2 分，满分 20 分。答案写在答题纸上）。 (1)若是矩阵的特性值，则 。(2)若是可逆矩阵的一种特性值，则必有一种特性值为 。 (3)若与相似，则 。(4)若矩阵与矩阵相似，则的特性值为 。(5)若为实对称矩阵，与是 的分别属于特性值 3 与 4的特性向量，则 。(6)设是实对称矩阵的分别属于特性值 1 和 2 的单位特性向量，则 。 (7)若是正交矩阵，是长度分别为的正交向量，则 。(8)二次型的秩是 。(9)二次型的符号差为 。(10)二次型的正惯性指数和秩的乘积是 。二、选择题(本题共 10 个小题,每小题 2 分，满分 20 分。每小题给出的四个选项中，只有一项是符合题目规定的。答案写在答题纸上)。(1)设为阶实对称矩阵，则 (A) ) 对于任意维实向量有 (B) 有个互相正交的特性向量；(C) 的线性无关的两个特性向量一定正交；(D 有个互不相似的的实特性值；(2)下列矩阵中不是正交矩阵的是 (3) 阶矩阵与对角矩阵相似的充足必要条件是(A) 有个互不相似的特性值； (B) 有个线性无关的特性向量；(C) 有个互不相似的特性向量； (D) 有个两两正交的特性向量。(4)同价矩阵与相似的充足必要条件是 (A)存在可逆矩阵与，使得；(B) 存在可逆矩阵，使得；(C) 存在可逆矩阵，使得； (D) 。(5)如果矩阵与对角矩阵相似，则 [ ](A)； (B)； (C)； (D) 。(6) 若实可逆矩阵使得实矩阵满足，则必成立[ ](A)与有相似的特性值; (B) 当 是对称矩阵时，有;(C)当时，二次型与有相似的规范形； (D) 与相似。(7)实二次型正定的一种充足必要条件是 [ ] (A); (B)存在可逆矩阵，使得成为对角形矩阵；(C)可逆； (D)存在可逆矩阵，使得。(8)二次型的一种原则形是 [ ](A); (B) ; (C) ； (D) 。 (9)设则[ ] (A)与既合同又相似； (B) 与合同但不相似；(C) 与不合同但相似；(D) 与既不合同又不相似。(10)设是三阶矩阵，将 的第二行加到第一行得，将的第二列减去第一列得，记，则[ ](A)； (B)；(C)； (D)。三、计算题(本题共 5 个小题，满分为 40 分) (解答写在答题纸上) (1)(5 分)设，求(i);(ii)。 (2)(5 分)设阶实对称矩阵的特性值是，求(i)(ii);(iii)的最小特性值；(iv)二次型的正惯性指数。(3)(10 分)设，求可逆矩阵，使...