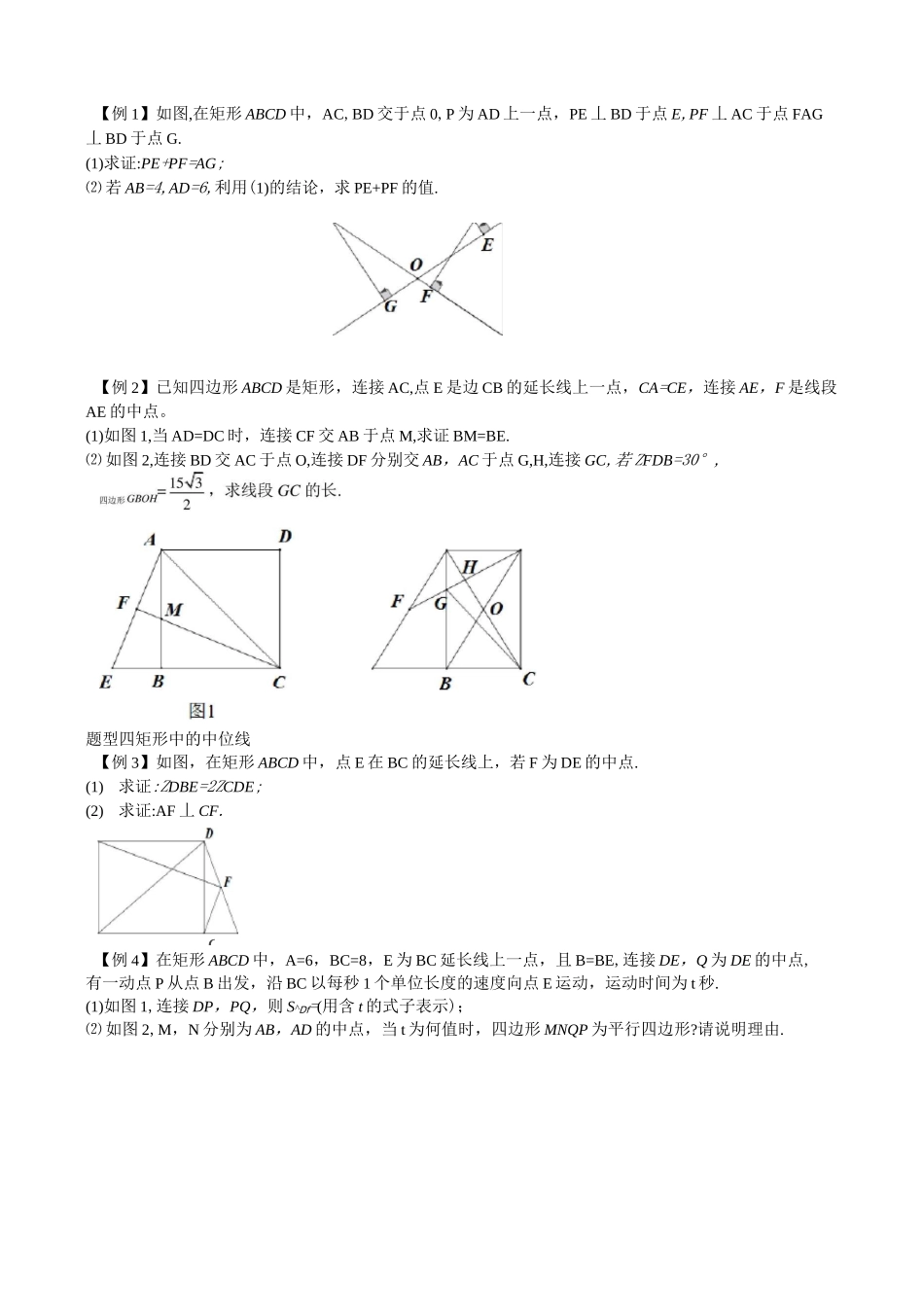
第 10 讲矩形知识导航1•矩形是特殊的平行四边形,具有平行四边形的所有性质;2•矩形的四个角都是直角,矩形的对角线相等,矩形是轴对称图形,又是中心对称图形;3•矩形的判定:有三个角是直角的四边形是矩形;对角线相等的平行四边形是矩形;对角线相等且互相平分的四边形是矩形.【板块一】矩形的折叠问题方法技巧矩形的折叠图中,有较多的直角三角形,常运用相等的边、勾股定理计算边的长.题型一矩形折叠一一勾股定理求边长【例 1】已知矩形 ABCD 中,AB=4,BC=3,按下列要求折叠:⑴ 如图 1,把矩形 ABCD 沿对角线 BD 折叠得△EBD’BE 交 CD 于点 F,求 DF 的长;⑵ 如图 2,折叠矩形 ABCD,使 AD 落在对角线 BD 上,求折痕 DE 的长;⑶ 如图 3,折叠矩形 ABCD,使点 B 与点 D 重合,求折痕 EF 的长.【例 2】如图,在矩形 ABCD 中,E 是 BC 的中点,将 AABE 沿 AE 折叠后得到 AAFE,点 F 在矩形 ABCD内部,延长 AF 交 CD 于点 G.(1)猜想线段 GF 与 GC 有何数量关系?并证明你的结论;⑵ 若 AB=3,AD=4,求线段 GC 的长.题型二矩形折叠一一求边的比值【例 3】如图 1,在 OABCD 中,E 是 AD 上一点,连接 CEF 为 CE 的中点,DF=EF.(1)求证:四边形 ABCD 为矩形;⑵ 如图 2,若 AE=AB,过点 B 作 BG 丄 CE,垂足为点 G,连接 AG.求 ZAGB 的度数。@I针对练习 11•如图,在矩形纸片 ABCD 中 AB=4,BC=8,将纸片沿 EF 折叠,使点 C 与点 A 重合,求 EF 的长.2.如图,在正方形 ABCD 中,E 为 AB 边上一点,过点 D 作 DF 丄 DE,与 BC 的延长线交于点,连接 EF,与CD 边交于点 G,与对角线 BD 交于点 H.(1) 若 BF=BD=还求 BE 的长;(2) 若 ZADE=2ZBFE,求证:FH=HE+HD.3.(1)【操作发现】如图,在矩形 ABCD 中,点 E 是 AD 的中点,将 AABE 沿 BE 折叠后到 AGBE,且点 G 在矩形 ABCD 内部,将 BG 延长交 DC 于点 F,小明认为 GF=DF,你同意吗?请说明理由.⑵【问题解决】保持⑴中的条件不变,若 DC=2DF,求型的值.AB⑶【类比探究】保持⑴中的条件不变,若 DC=nDF,直接写出型的值:.AB【板块二】矩形与等腰三角形方法技巧1•利用矩形的性质可证明线段相等或平分,角相等,两直线平行或垂直,还可以求角的度数;2•矩形的对角线将矩形分成两对全等的等腰三角形,因此矩形有关问题常常会用到等腰三角形的性质.题型三矩形中的...