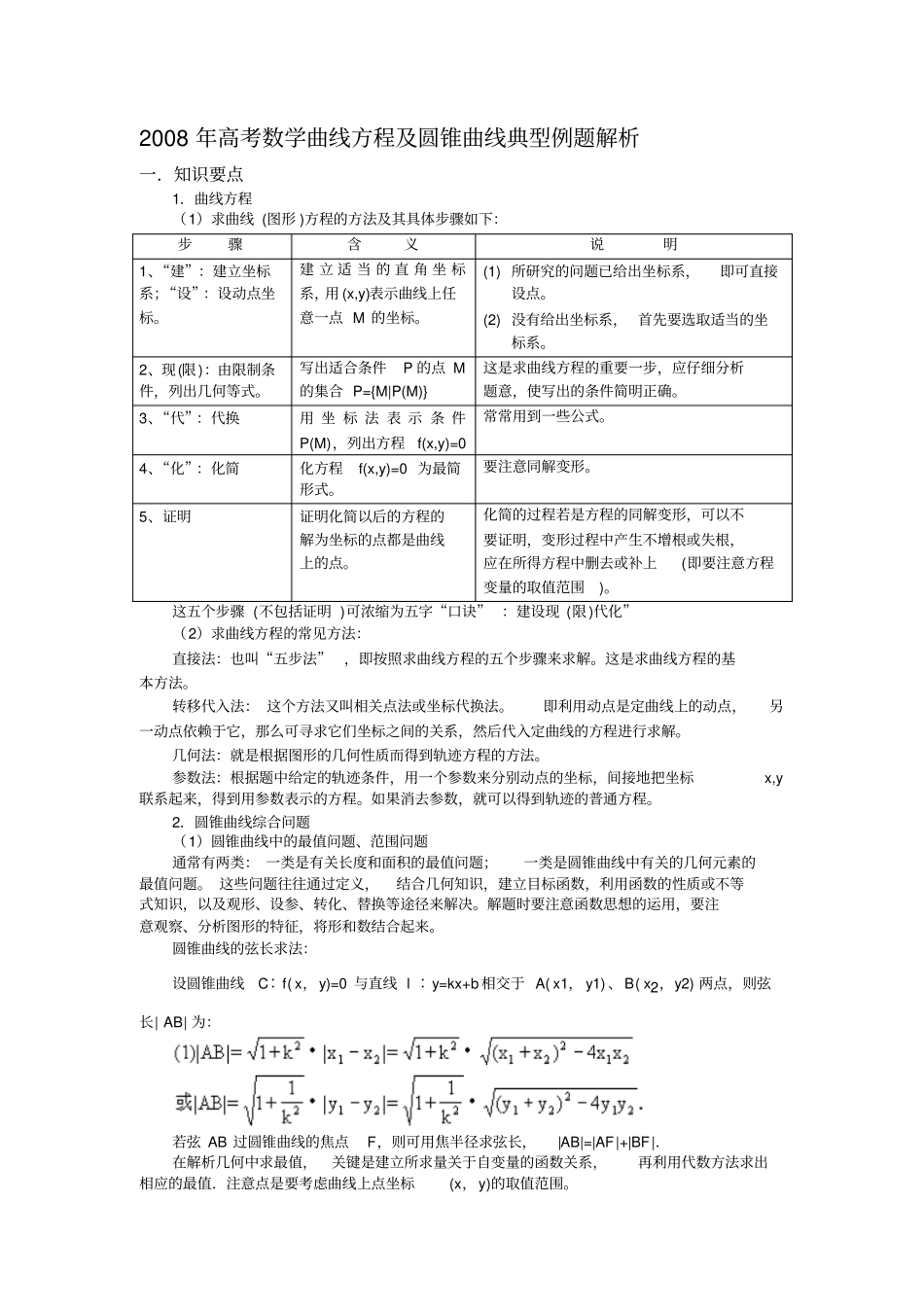
2008 年高考数学曲线方程及圆锥曲线典型例题解析一.知识要点1.曲线方程(1)求曲线 (图形 )方程的方法及其具体步骤如下:步骤含义说明1、“建”:建立坐标系;“设”:设动点坐标。建 立 适 当 的 直 角 坐 标系,用 (x,y)表示曲线上任意一点 M 的坐标。(1) 所研究的问题已给出坐标系,即可直接设点。(2) 没有给出坐标系, 首先要选取适当的坐标系。2、现(限):由限制条件,列出几何等式。写出适合条件P 的点 M的集合 P={M|P(M)} 这是求曲线方程的重要一步,应仔细分析题意,使写出的条件简明正确。3、“代”:代换用 坐 标 法 表 示 条 件P(M),列出方程f(x,y)=0 常常用到一些公式。4、“化”:化简化方程f(x,y)=0 为最简形式。要注意同解变形。5、证明证明化简以后的方程的解为坐标的点都是曲线上的点。化简的过程若是方程的同解变形,可以不要证明,变形过程中产生不增根或失根,应在所得方程中删去或补上(即要注意方程变量的取值范围)。这五个步骤 (不包括证明 )可浓缩为五字“口诀” :建设现 (限)代化”(2)求曲线方程的常见方法:直接法:也叫“五步法”,即按照求曲线方程的五个步骤来求解。这是求曲线方程的基本方法。转移代入法: 这个方法又叫相关点法或坐标代换法。即利用动点是定曲线上的动点,另一动点依赖于它,那么可寻求它们坐标之间的关系,然后代入定曲线的方程进行求解。几何法:就是根据图形的几何性质而得到轨迹方程的方法。参数法:根据题中给定的轨迹条件,用一个参数来分别动点的坐标,间接地把坐标x,y联系起来,得到用参数表示的方程。如果消去参数,就可以得到轨迹的普通方程。2.圆锥曲线综合问题(1)圆锥曲线中的最值问题、范围问题通常有两类: 一类是有关长度和面积的最值问题;一类是圆锥曲线中有关的几何元素的最值问题。 这些问题往往通过定义,结合几何知识,建立目标函数,利用函数的性质或不等式知识,以及观形、设参、转化、替换等途径来解决。解题时要注意函数思想的运用,要注意观察、分析图形的特征,将形和数结合起来。圆锥曲线的弦长求法:设圆锥曲线C∶f( x,y)=0 与直线 l ∶y=kx+b 相交于 A( x1, y1) 、B( x2,y2) 两点,则弦长| AB| 为:若弦 AB 过圆锥曲线的焦点F,则可用焦半径求弦长,|AB|=|AF|+|BF|.在解析几何中求最值,关键是建立所求量关于自变量的函数关系,再利用代数方法求出相应的最值.注意点是要考虑曲线上点坐标(x,y)的...