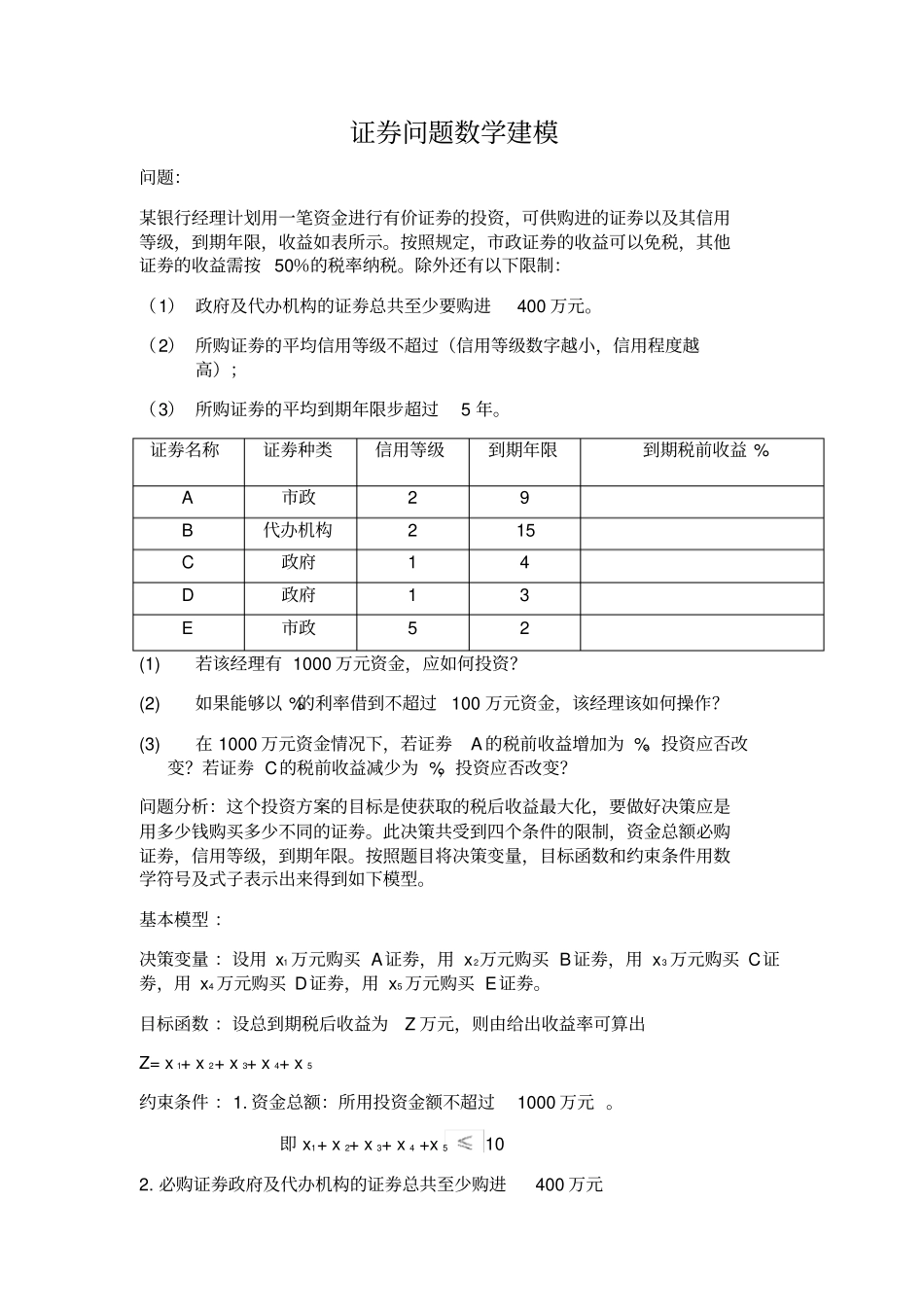
证券问题数学建模问题:某银行经理计划用一笔资金进行有价证劵的投资,可供购进的证劵以及其信用等级,到期年限,收益如表所示。按照规定,市政证劵的收益可以免税,其他证劵的收益需按 50%的税率纳税。除外还有以下限制:(1) 政府及代办机构的证劵总共至少要购进400 万元。(2) 所购证劵的平均信用等级不超过(信用等级数字越小,信用程度越高);(3) 所购证劵的平均到期年限步超过5 年。证劵名称证劵种类信用等级到期年限到期税前收益 %A市政29B代办机构215C政府14D政府13E市政52(1)若该经理有 1000 万元资金,应如何投资?(2)如果能够以 %的利率借到不超过100 万元资金,该经理该如何操作?(3)在 1000 万元资金情况下,若证劵A 的税前收益增加为 %。投资应否改变?若证劵 C的税前收益减少为 %,投资应否改变?问题分析:这个投资方案的目标是使获取的税后收益最大化,要做好决策应是用多少钱购买多少不同的证劵。此决策共受到四个条件的限制,资金总额必购证劵,信用等级,到期年限。按照题目将决策变量,目标函数和约束条件用数学符号及式子表示出来得到如下模型。基本模型 :决策变量 :设用 x1 万元购买 A证劵,用 x2万元购买 B证劵,用 x3 万元购买 C证劵,用 x4 万元购买 D证劵,用 x5 万元购买 E证劵。目标函数 :设总到期税后收益为Z 万元,则由给出收益率可算出Z= x 1+ x 2+ x 3+ x 4+ x 5 约束条件 :1. 资金总额:所用投资金额不超过1000 万元 。即 x1+ x 2+ x 3+ x 4 +x 5102. 必购证劵政府及代办机构的证劵总共至少购进400 万元即 x2+ x 3+ x 443. 信用等级:所购证劵的平均信用等级都不超过,即4. 到期年限:所购证劵的平均到期年限步超过5 年,即5. 非负约束 x1 x 2 x 3 x 4x5为输入方便,将( 3)( 4)化简可得到该问题的基本模型 Max Z= x1+ x 2+ x 3+ x 4+ x 5 (1)x1 +x 2+ x 3+ x 4 +x 510(2)x2+ x 3+ x 44 (3) 6x1+ 6x 2-4x 3-4x 4 +36x 510 (4) 4x 1+10 x 2- x3-2x 4 -3x510 (5)x1 x 2 x 3 x 4x5模型求解 :用 LINGO软件求解输入:model:max= *x 1+* x2+* x3+* x4+* x5 ;[money] x1+ x 2+ x 3+ x 4 +x 510;[must] x2+ x 3+ x 44;[credit] 6*x 1+ 6*x 2-4*x 3-4*x 4 +36*x 50;[time] 4*x1+10*x 2-x 3-2*x 4 -3*x50 ;end得到如下输出 :Global...