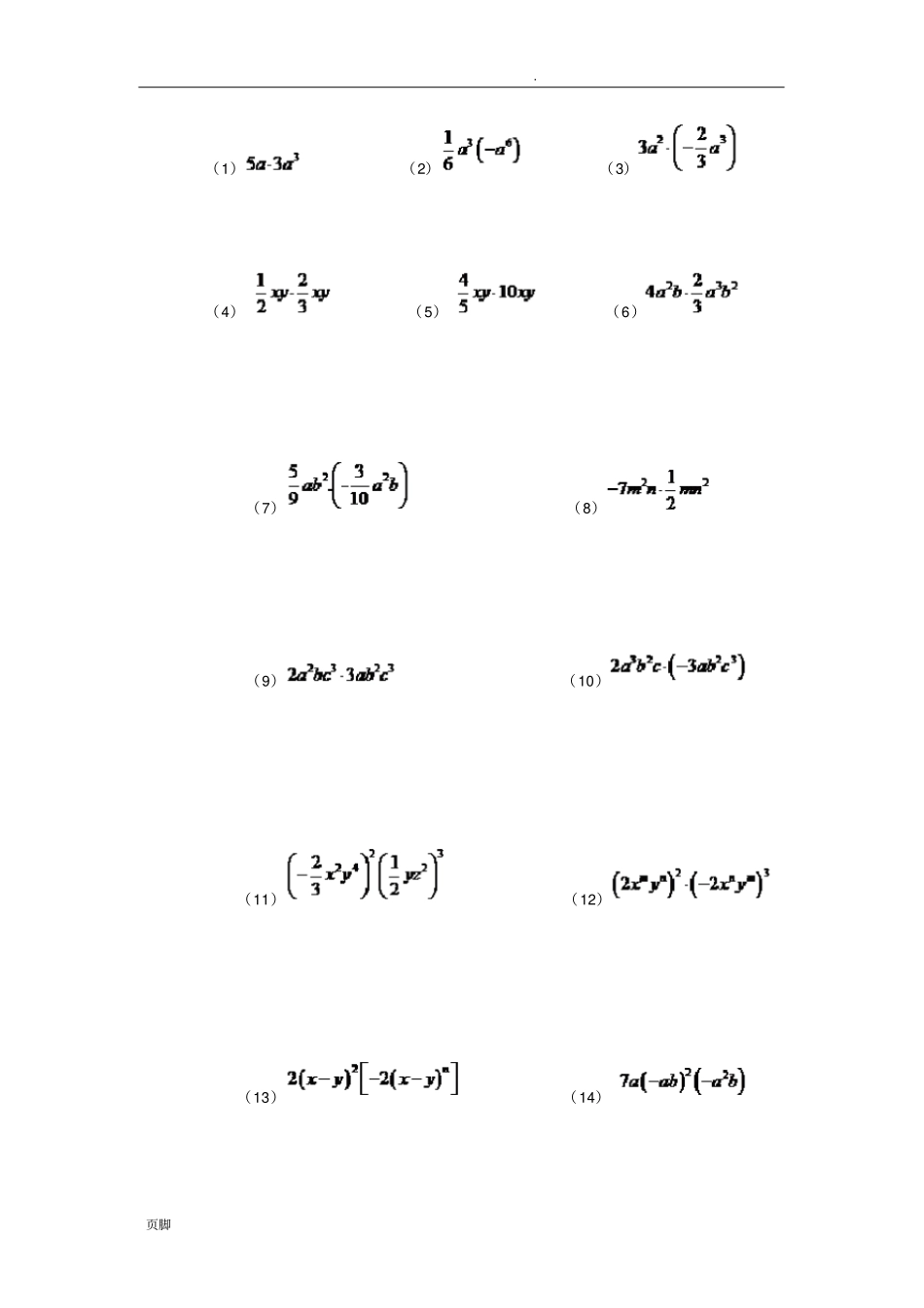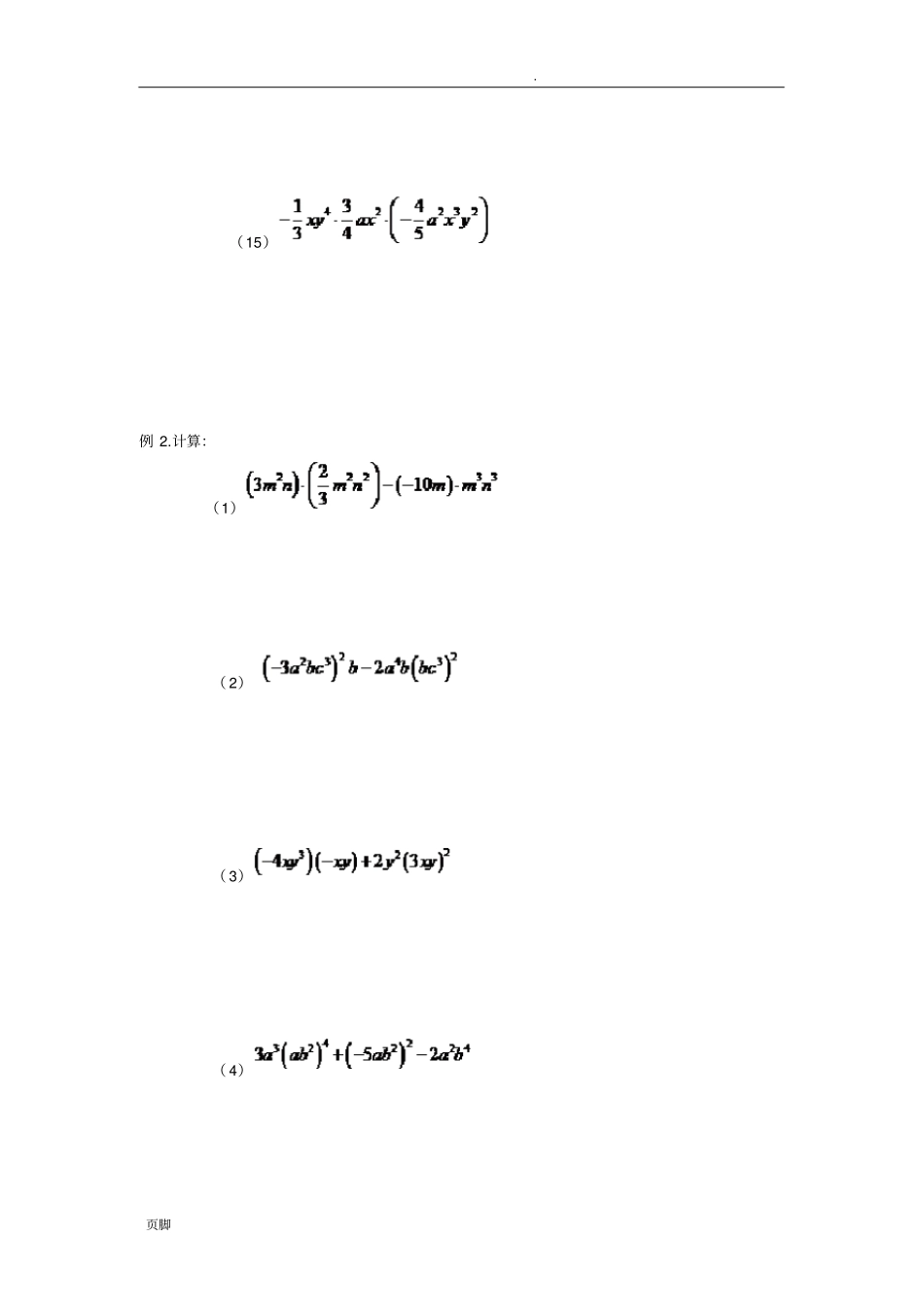. 页脚整式的乘法注意: 单项式的乘法的关键是通过乘法的交换律和结合律,把它转化为幂的运算.单项式与多项式的乘法可以采用我们已经熟悉的有理数运算中乘法分配律的应用类比理解,并且指导运算.多项式与多项式的乘法,先将一个多项式的每项分别与另外一个多项式的每项相乘,再把所得的积相加,运算中利用单项式与单项式的乘法和合并同类项.运算时需要按照一定的顺序进行,防止漏项和符号出错.1.单项式的概念: 由数与字母的乘积构成的代数式叫做单项式.单独的一个数或一个字母也是单项式 .单项式的数字因数叫做单项式的系数,字母指数和叫单项式的次数. 2.多项式的概念: 几个单项式的和叫做多项式.多项式中每个单项式叫做多项式的项,次数最高的项的次数叫多项式的次数. 3.整式的概念:单项式和多项式统称整式. 注意: 凡是分母含有字母的代数式都不是整式,也不是单项式和多项式. 4.单项式与单项式相乘的法则:把它们的系数、同底数幂分别相乘的积作为积的因式,其余字母连同它的指数不变,也作为积的因式. 注意:(1)① 积的系数等于各因式系数的积;② 相同字母相乘是同底数幂的乘法,按照“底数不变,指数相加”计算;③ 只在一个单项式里含有的字母,要连同它的指数写在积里,要注意不要丢掉这个因式;④ 单项式乘以单项式的结果仍是单项式;⑤ 单项式乘法法则对于三个以上的单项式相乘同样适用. (2)单项式乘法中,若有乘、乘法等混合运算,应按“先乘、再乘法”的顺序进行. 例 1.计算 :. 页脚(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14). 页脚(15)例 2.计算:(1)( 2)( 3)( 4). 页脚(5)( 6)(7)(n 是正整数)例 3.先化简,后求值:,其中. . 页脚例 4.已知,求的值 . 5.单项式与多项式相乘的法则:使用单项式乘以多项式的每项,再把所得的积相加. 注意:(1)法则中“每项”是指含有性质符号的项;(2)单项式乘以多项式,它的积仍为多项式,项数与原多项式(没有同类项)的项数相同,不要漏乘项;(3)乘积中符号的确定与括号法则基本一致,括号前的单项式系数为正数,去括号后多项式各项的符号都不变,否则都改变;(4)对混合运算应该注意运算顺序,并且有同类项时,必须合并同类项,从而得到最简结果;(5)由法则可以看出: 单项式与多项式相乘就是根据乘法分配律把问题转化为单项式的乘法,它的思路是例 5.计算 : (1)( 2)(...