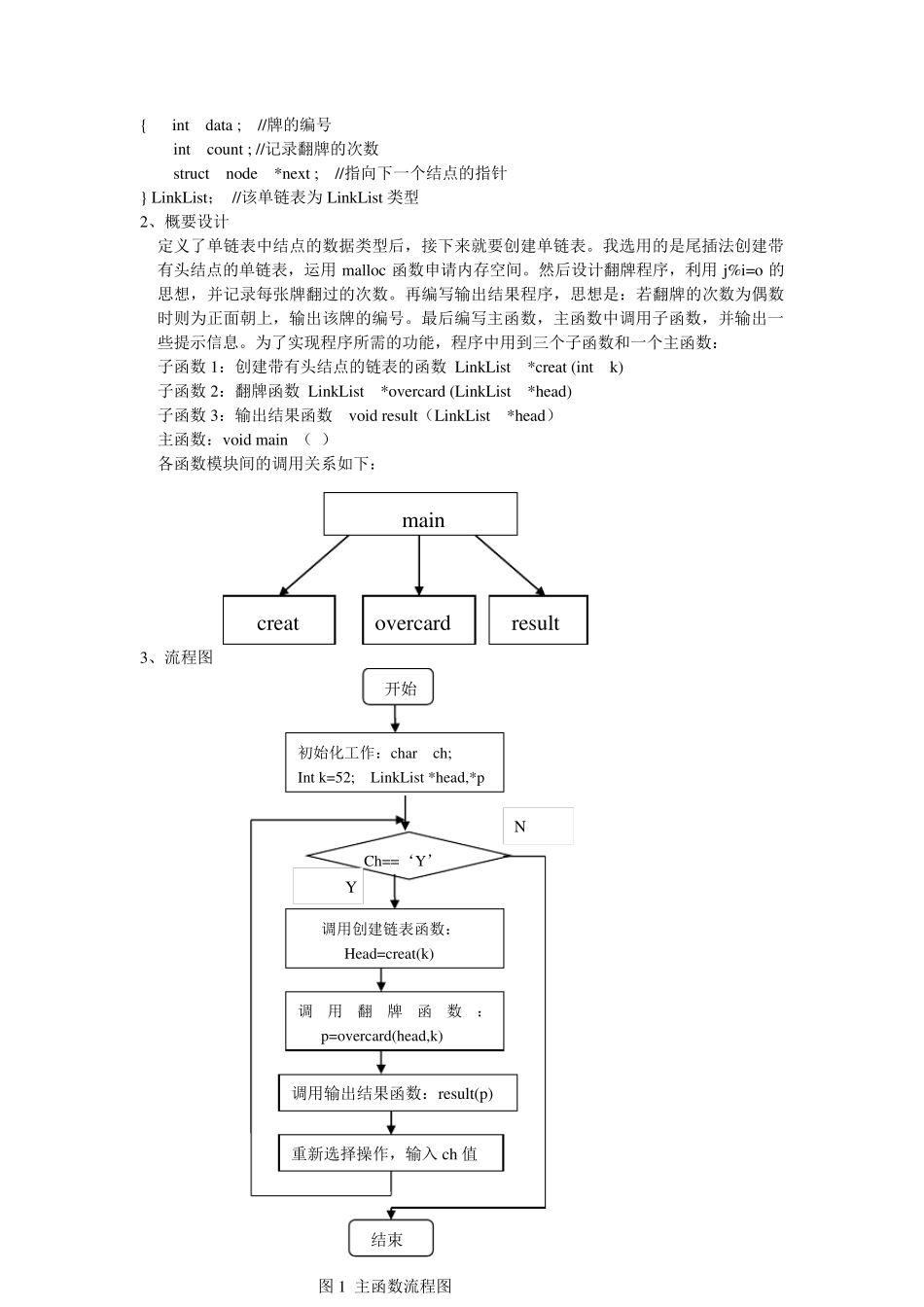
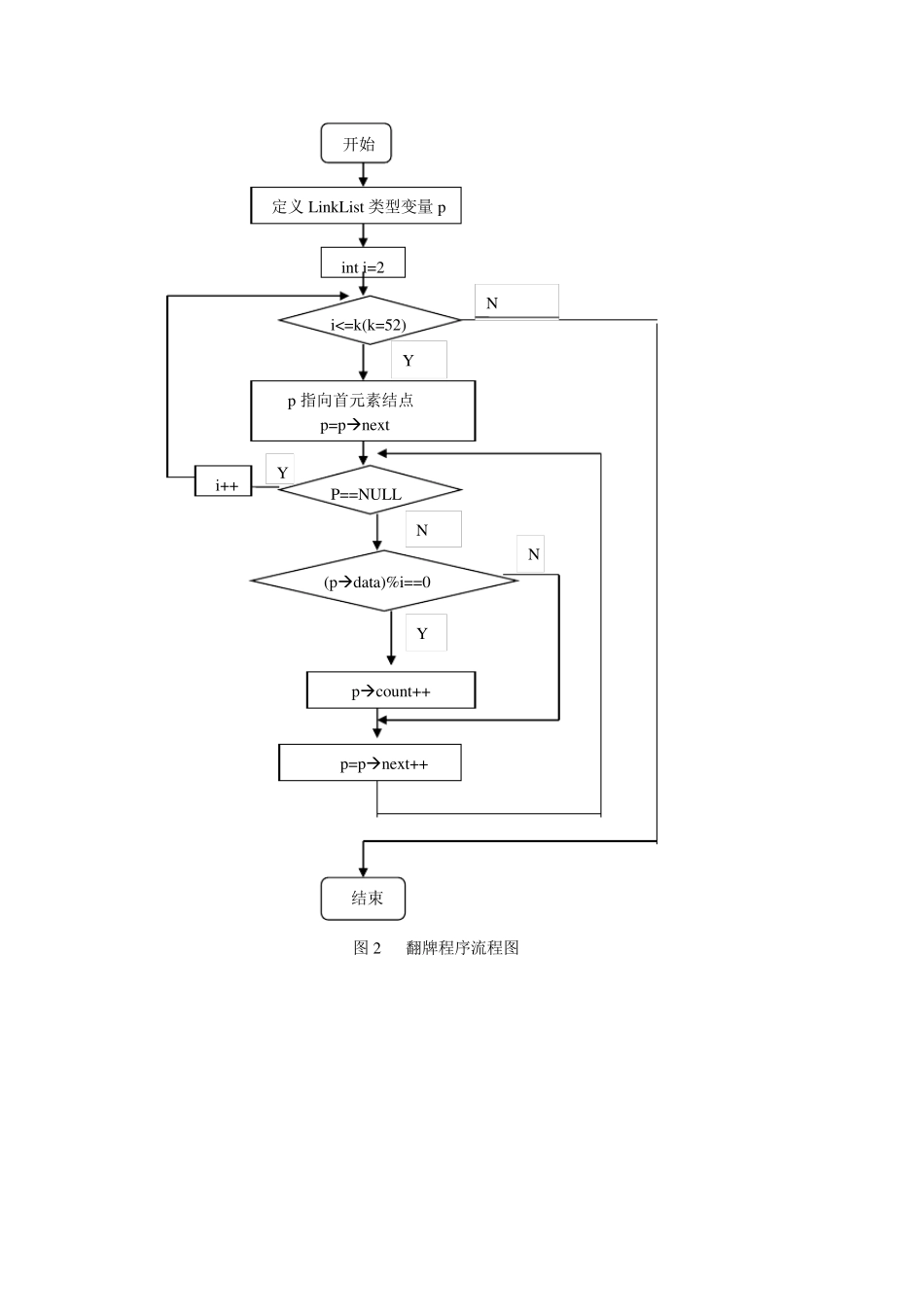
题目:(纸牌游戏)编号为1~52 张牌,正面向上,从第二张开始,以2 为基数,是2的倍数的牌翻一次,直到最后一张牌;然后从第三张牌开始,以3 为基数,是3 的倍数的牌翻一次,直到最后一张牌;直到以52 为基数的翻过,输出:这时输出正面向上的牌有哪些? 一、问题分析及任务定义 1、 此程序需要完成如下要求:有已编号的1~52 张牌且正面朝上,从第二张牌开始,以2 为基数,是2 的倍数的牌翻一次,直到最后一张牌;直到以52 为基数的牌翻过,要求最后输出所有正面向上的牌的编号。 2、 任务定义:实现本程序需要解决以下几个问题: ① 如何存储 52 张牌,所选择的存储结构要便于实现题给要求的操作。 ② 如何设计翻牌程序。 ③ 一张牌可能一次未翻,也可能翻多次,在经过所有的翻牌以后,如何知道每一张牌是否为正面向上。 ④ 输出所有正面向上的牌的编号。 本问题的关键在于选择合适的数据结构存储 52 张牌,难点在于在所选的数据结构下实现题给要求的翻牌操作。另一个难点在于所有的牌都进行了翻牌操作后,如何知道每一张牌是否为正面向上。 首先我们可以从实际生活中的操作来探讨第二个难点的解决思路。编号为1 的牌没有进行翻牌,即翻牌的次数为0,仍然为正面朝上;编号为2 的牌在整个过程中只翻了一次,为反面朝上;编号为3 的牌在整个过程中只翻了一次,为反面朝上;编号为4 的牌在整个过程中翻了两次,为正面朝上;编号为5 的牌在整个过程中翻了一次,为反面朝上;编号为6 的牌在整个过程中翻了三次(由于 6 是2、3、6 的倍数),为反面朝上;以此类推直至编号为52 的牌,从上述过程可以总结出这样的规律:从编号为1 的第一张牌到编号为52 的最后一张牌,只要它翻过的次数为偶数则是正面朝上,反之则为反面朝上。因此我们可以依据每张牌翻过的次数来确定它最终是否为正面向上,从而输出实验所需要的结果 :所有正面向上的牌的编号。 3、原 始数据的输入 、输出格 式 :由于本程序简 单 明 了,不 需要有任何的数据输入 ,只须 用户 选择执 行或 不 执 行此程序,若 执 行此程序,在程序运 行后便可直接 在运 行结果 窗 口 中看 到所有正面朝上的牌的编号,这些编号数据均 为整型 ;若 不 执 行该 程序则选择退 出。 二、数据结构的选择和 概 要设计 1、数据结构的选择 因为编号为1~52 的52 张牌没有要求在物 理 位 置 上相 邻 接 ,且在翻牌操作...