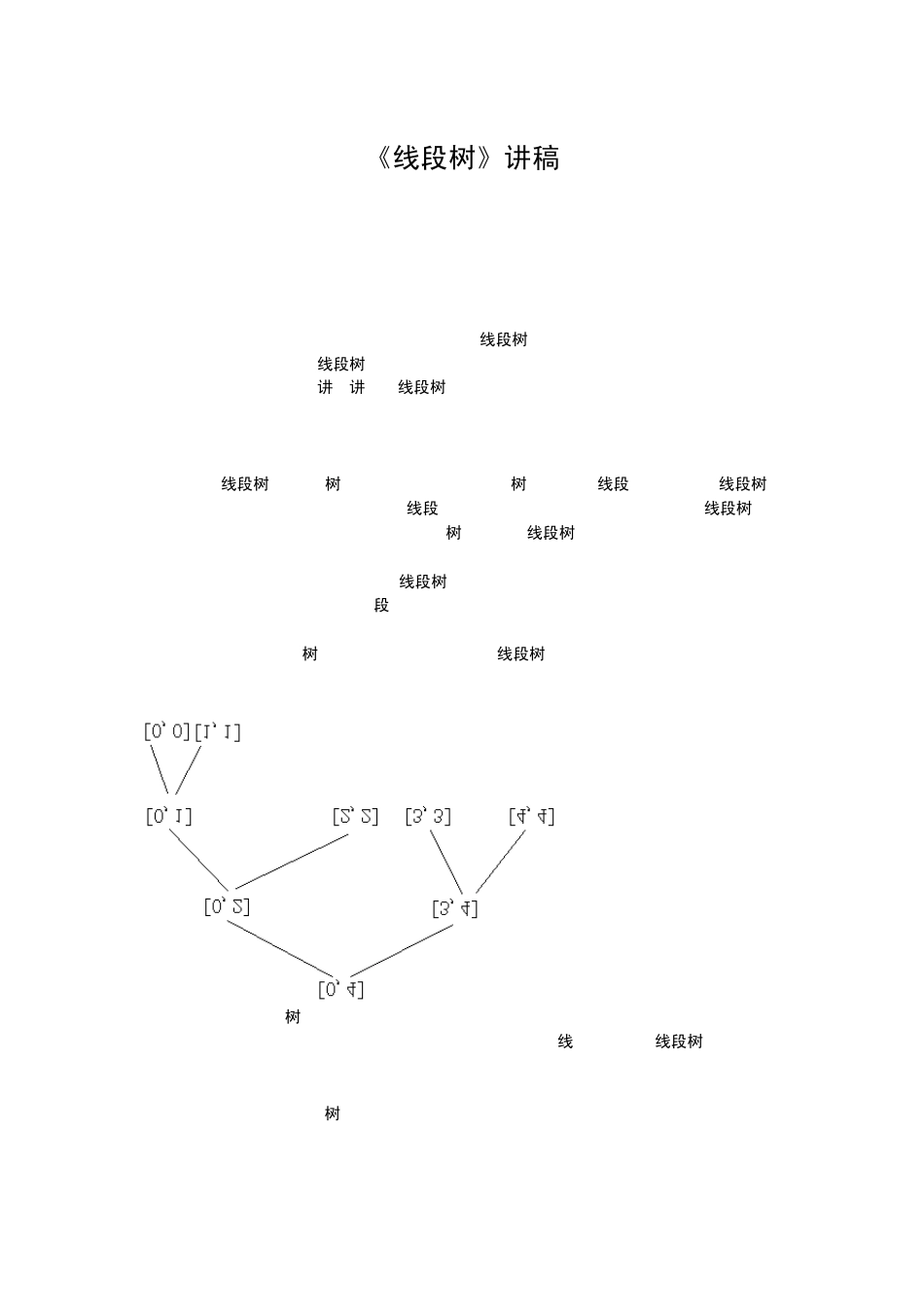
《线段树》讲稿安徽师范大学附属中学杨弋前言在谈论到种种算法知识与数据结构的时候,线段树无疑总是与“简单”和“平常”联系起来的。而这些特征意味着,线段树作为一种常用的数据结构,有常用性,基础性和易用性等诸多特点。因此,今天我来讲一讲关于线段树的话题。定义首先,线段树是一棵“树”,而且是一棵完全二叉树。同时,“线段”两字反映出线段树的另一个特点:每个节点表示的是一个“线段”,或者说是一个区间。事实上,一棵线段树的根节点表示的是“整体”的区间,而它的左右子树也是一棵线段树,分别表示的是这个区间的左半边和右半边。在此我们可以举一个例子来说明线段树通常的构造方法,以 RMQ问题为例:有N个数排成一排,每次询问某一段中的最小数。构造的时候,让根节点表示区间[0,N-1],即所有N个数所组成的一个区间,然后,把区间分成两半,分别由左右子树表示。不难证明,这样的线段树的节点数只有2N-1个,是O(N)级别的,如图:对于每个节点,不但要知道它所表示的区间,以及它的儿子节点的情况,也记录一些别的值,不然,一棵孤零零的树能有什么用?在这个例子里,由于要查询的东西是最小值,不妨在每个节点内记录下它所表示区间中的最小值。这样,根据一个线性表构造出线段树的方法也就简单明白了:function构造以v为根的子树ifv所表示的区间内只有一个元素v区间的最小值就是这个元素 ,构造过程结束endif把v所属的区间一分为二,用w和x两个节点表示。标记v的左儿子是 w,右儿子是 x分别构造以 w和以x为根的子树(递归)v区间的最小值<-min(w区间的最小值,x区间的最小值)endfunction这样,一棵线段树就建立好了。不难证明构造过程是O(n)的,而线段树的高度是O(logn)的,准确地说,就是|log2(n-1)|+1。由构造过程可以发现,修改单个元素的操作异常简单:functionmodify(v,i,newvalue)//把i的值修改为newvalue,当前处理的子树根节点是vifv所表示的区间内只有一个元素//这个元素必定表示的就是[i,i]v区间的最小值<-newvalue退出函数endifif(i属于v的左儿子的区间)modify(v的左儿子,i,newvalue)elsemodify(v的右儿子,i,newvalue)endifv区间的最小值<-min(w区间的最小值,x区间的最小值)//更新数据endfunction由于每个节点都至多递归一次,它的时间复杂度 =O(树深度)=O(logn)。区间查询操作继续上面的例子,由于RMQ的目的是在区间内查询最小值,现在讨论如何利用刚刚构造出来的线段树高效回答这一提问:比如刚才图中所示的树...