结构力学位移法专题讲解VIP免费

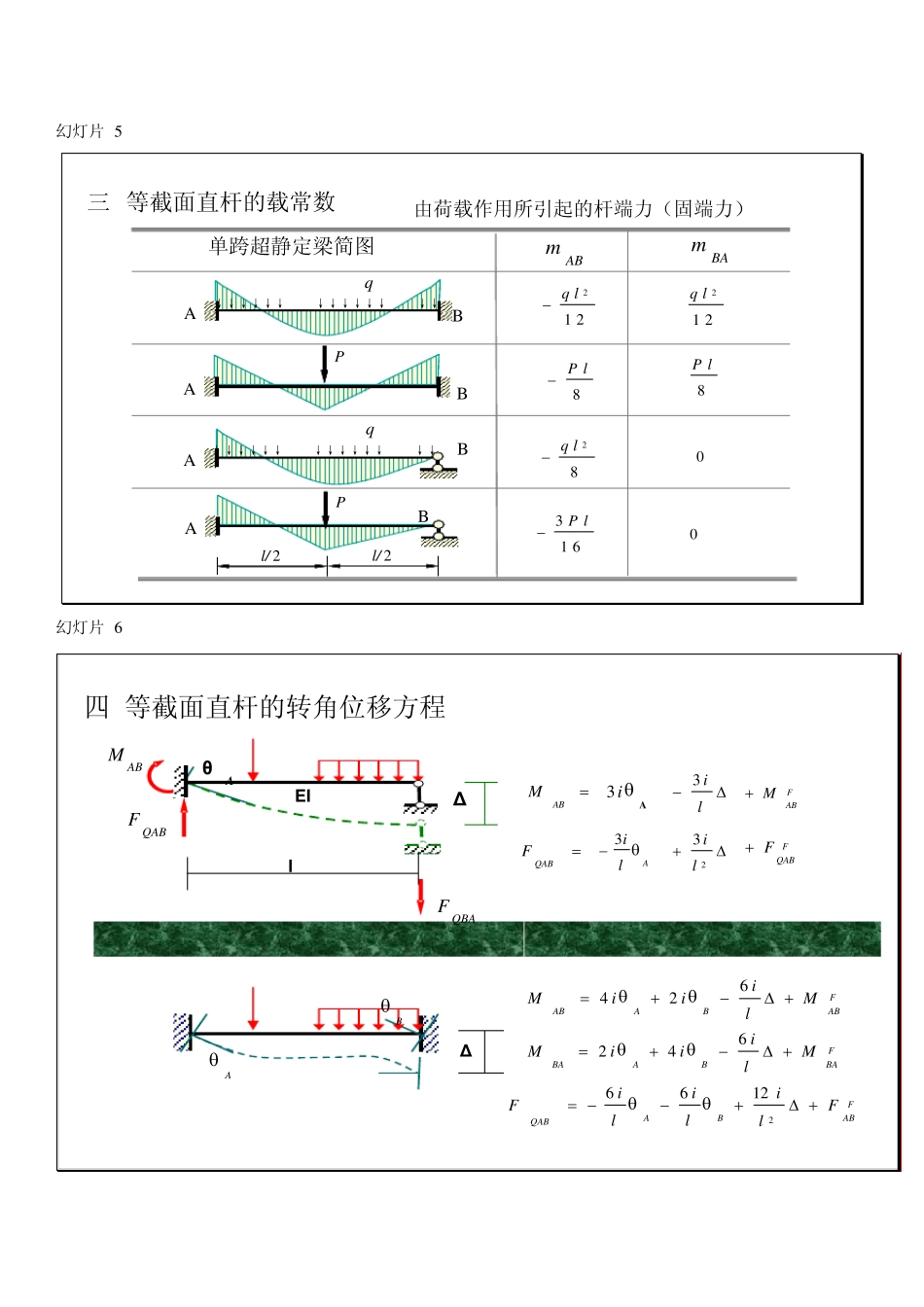
(结构力学)位移法专题讲解 §7-1 等截面直杆的转角位移方程一杆端位移与杆端力正负规定2 杆端相对位移Δ1 杆端转角θA、θBl——弦转角ABΔ以顺时针转动为正MABMBAFQABFQBA1 杆端弯矩MAB、MBA对杆端以顺时针为正2 杆端剪力FQAB、FQBA 使分离体有顺时针转动趋势时为正MABMBAFQABFQBAM ＞０ABM ＞０BA以顺时针转动为正l 幻灯片 3 由单位杆端位移所引起的杆端力（刚度系数）二 等截面直杆的形常数Δ =1θA =1EI3ili3Δ =1θA =1EI4i2ili6li6幻灯片 4 等截面直杆的形常数单跨超静定梁简图MABMBAQAB= QBA4i2iθ =1ABAB1212lili6li6li6AB10li3ABθ =13i023liABθ =1i－i0li3 幻灯片 5 三等截面直杆的载常数 由荷载作用所引起的杆端力（固端力）单跨超静定梁简图m ABm BAABAB↓↓↓↓↓↓↓↓↓↓↓↓↓↓q21 2ql21 2qlP8P l8P lAB↓↓↓↓↓↓↓↓↓↓↓↓↓↓q28qlABl/ 2l/ 2P31 6P l00 幻灯片 6 四 等截面直杆的转角位移方程θAΔMABFQABFQBAlEIABMAi3li3FABMQABFAli 323liFQABFABΔFBABABAFABBAABMliiiMMliiiM642624FABBAQABFlililiF21266幻灯片 7 § 7-2 位移法的基本概念一 位移法基本思路θＢqLLABCEIEIEILABθＢEILBCθＢq1 位移法基本未知量θB： 设顺时针方向转动2 各杆转角位移方程BBAlEIM30ABM832q llEIMBBC0ABM幻灯片 8 3 建立位移法方程0BCBABMMM0862 q llEIBEIq lB483BBAMBCMθＢqLLABCEIEI4 作弯矩图1648323q lEIq llEIMBA168483223q lq lEIq llEIMBC162q l幻灯片 9 θCθDΔCΔD§ 7-3 位移法基本结构与未知量数目CD一位移法基本未知量 1 结点角位移为了减小计算工作量、简化计算，引入如下假定：①忽略轴力产生的轴向变形，②结点转角、各杆弦转角都很微小受弯直杆变形前后，两端之间的距离保持不变ΔΔ2 独立结点线位移Δ C、Δ D对应一个独立结点线位移Δ 幻灯片 1 0 铰接链杆体系几何可变体系几何不变体系附加链杆的数目 =独立结点线位移的数目独立结点线位移数目的确定 幻灯片 1 1 § 7-3 位移法基本结构与未知量数目1 附加刚臂2 附加链杆控制结点线位移θCθDΔCΔDCD控制结点转动基本结构二位移法基本结构幻灯片 1 2 θCθDΔCΔDCDZ1Z2基本结构结点角位移的数目=刚结点的数...