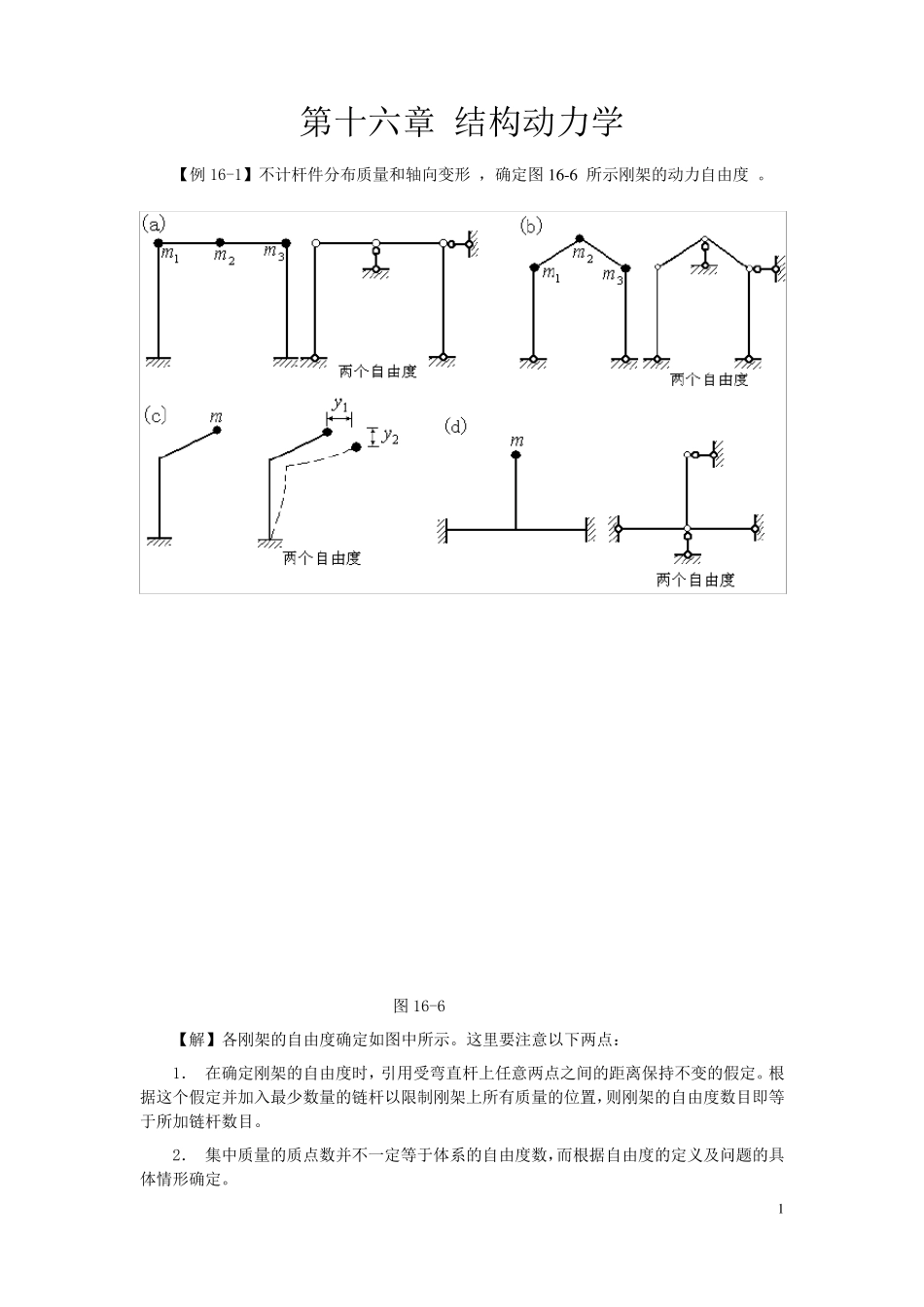
1 第十六章 结构动力学 【例16-1】不计杆件分布质量和轴向变形 ,确定图1 6 -6 所示刚架的动力自由度 。 图16-6 【解】各刚架的自由度确定如图中所示。这里要注意以下两点: 1. 在确定刚架的自由度时,引用受弯直杆上任意两点之间的距离保持不变的假定。根据这个假定并加入最少数量的链杆以限制刚架上所有质量的位置,则刚架的自由度数目即等于所加链杆数目。 2. 集中质量的质点数并不一定等于体系的自由度数,而根据自由度的定义及问题的具体情形确定。 2 【例16-2】 试用柔度法建立图16-7a 所示单自由度体系,受均布动荷载)t(q作用的运动方程。 【解】本题特点是,动荷载不是作用在质量上的集中荷载。对于非质量处的集中动荷载的情况,在建立运动方程时,一般采用柔度法较为方便。 设图a 质量任一时刻沿自由度方向的位移为y(向下为正)。把惯性力I 、阻尼力R 及动荷载)(tP,均看作是一个静荷载,则在其作用下体系在质量处的位移y,由叠加原理(见图b、c、d 及 e),则 )(RIyPDIP 式中,)t(qEI38454P,EI483。将它们代入上式,并注意到ymI, ycR,得 )(48)(384534ycymEItqEIy 图16-7 经整理后可得 )(tPkyycymE 式中,3EI481k,)(85)(tqktPPE )(tPE称为等效动荷载或等效干扰力。其含义为:)(tPE直接作用于质量上所产生的位移和实际动荷载引起的位移相等。图a 的相当体系如图f 所示。 【例16-3】 图16-8a 为刚性外伸梁,C 处为弹性支座,其刚度系数为k ,梁端点A、D处分别有 m 和 3m质量,端点D 处装有阻尼器 c,同时梁 BD 段受有均布动荷载)t(q作用,试建立刚性梁的运动方程。 【解】 因为梁是刚性的,这个体系仅有一个自由度,故它的动力响应可由一个运动方程来表达,方程可以用直接平衡法来建立。 这个单自由度体系可能产生的位移形式如图b 所示,可以用铰 B 的运动)t(作为基本 3 量,而其它一切位移均可利用它来表示。 图16-8 )t(以顺时针向为正。则A 点有位移)t(2 和加速度)t(2 ;D 点有位移)t(23 和加速度)t(23 及速度)t(23 ;C 点约束反力为)t(kRc 。 由 0MB,有 043)(232323221tqRRIIC 将惯性力、阻尼力及约束反力代入上式,得 043)t(q23)]t(k[23)]t(c23[23)]t(3m23[2)]t(m2[2...