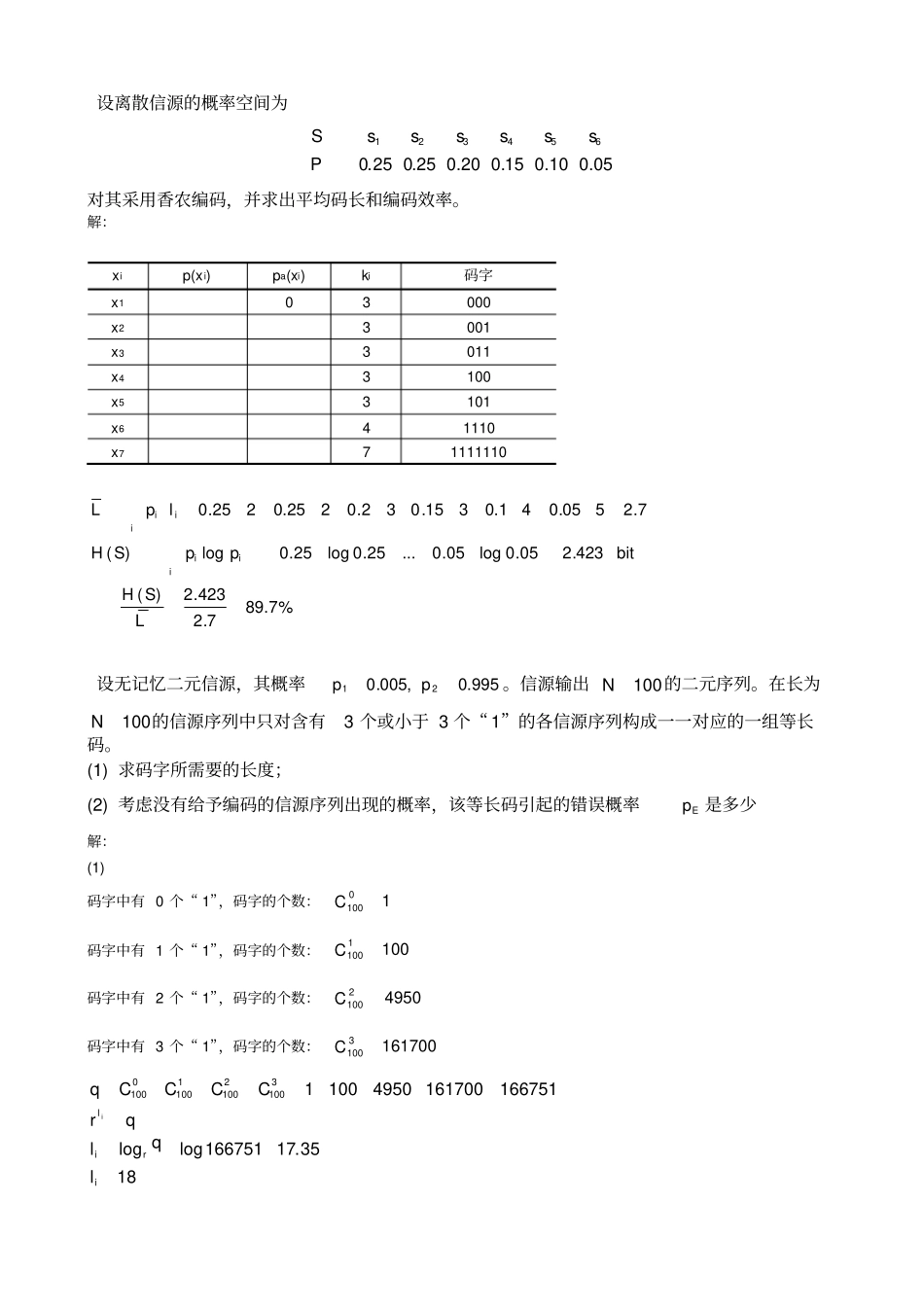
有一信源, 它有 6 个可能的输出, 其概率分布如题表所示, 表中给出了对应的码EDCBA,,,,和F 。题表消息p(a i) A BCDEFa11/200000000a21/400101101010100a31/160100111101101100101a41/160110111111011101101110a51/16100011111111010111100111a61/1610101111111111011011111011(1) 求这些码中哪些是唯一可译码;(2) 求哪些是非延长码(即时码) ;(3) 对所有唯一可译码求出其平均码长L 。解:(1) 唯一可译码: A,B,CA 是等长码,码长3,每个码字各不相同,因此是唯一可译码。B 是非即时码,前缀码,是唯一可译码。C 是即时码,是唯一可译码。D 是变长码,码长}4,4,4,3,2,1{,不是唯一可译码,因为不满足Kraft 不等式。10625.13212121214321il irE 是变长码,码长}4,4,4,4,2,1{,满足 Kraft 不等式,但是有相同的码字,110053WW,不是唯一可译码。114212121421il irF 是变长码,码长}3,3,3,3,3,1{,不满足 Kraft 不等式,不是唯一可译码。1125.15212131il ir(2) 非延长码: A,C(3)3125.161615161416131612411213iiiCBAlpLLL设离散信源的概率空间为05.010.015.020.025.025.0654321ssssssPS对其采用香农编码,并求出平均码长和编码效率。解:xip(xi)pa(xi)ki码字x103000x23001x33011x43100x53101x641110x771111110%7.897.2423.2)(423.205.0log05.0...25.0log25.0log)(7.2505.041.0315.032.0225.0225.0LSHbitppSHlpLiiiiii设无记忆二元信源,其概率995.0,005.021pp。信源输出100N的二元序列。在长为100N的信源序列中只对含有3 个或小于 3 个“ 1”的各信源序列构成一一对应的一组等长码。(1) 求码字所需要的长度;(2) 考虑没有给予编码的信源序列出现的概率,该等长码引起的错误概率Ep 是多少解:(1)码字中有 0 个“ 1”,码字的个数:10100C码字中有 1 个“ 1”,码字的个数:1001100C码字中有 2 个“ 1”,码字的个数:49502100C码字中有 3 个“ 1”,码字的个数:1617003100C1835.17166751loglog166751161700495010013100210011000100irillqlqrCCCCqis7s8s9s6s5s1s2s3s4s10s12s110.070.250.53(2)码字中有 0 个“ 1”,错误概率:100995.01ap码字中有 1 个“ 1”,错误概率:005.0995.0992ap码字中有 2 个“ 1”,错误概率:298500.0995.03ap码字中有 3 个“ 1”,错误概率:397500.0995.04ap0017.09983.0119983.0161700005.0995.04950005.0995.0100005.0995.01995.039729899100...