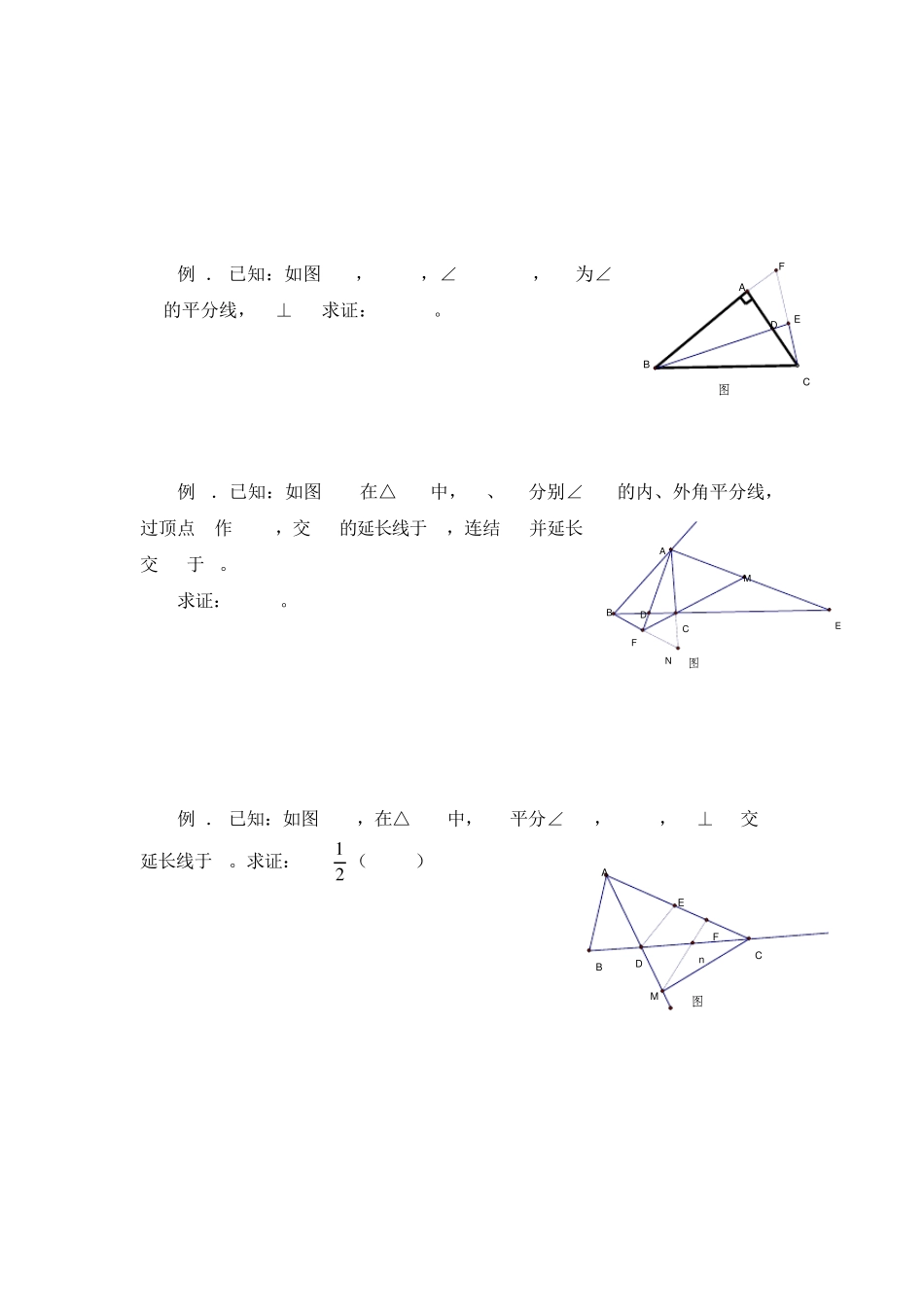
一、由角平分线想到的辅助线 口诀: 图中有角平分线,可向两边作垂线。也可将图对折看,对称以后关系现。角平分线平行线,等腰三角形来添。角平分线加垂线,三线合一试试看。 (一)、截取构全等 例1. 如图1-2,AB//CD,BE平分∠ABC,CE平分∠BCD,点 E在 AD上,求证:BC=AB+CD。 例2. 已知:如图1-3,AB=2AC,∠BAD=∠CAD,DA=DB,求证 DC⊥AC 例3. 已知:如图1-4,在△ABC中,∠C=2∠B,AD平分∠BAC,求证:AB-AC=CD 图1-2ADBCEF图1-3ABCDE图1-4ABCDE (二)、角分线上点向角两边作垂线构全等 例1. 如图2-1,已知AB>AD, ∠BAC=∠FAC,CD=BC。 求证:∠ADC+∠B=180 例2. 如图2-2,在△ABC中,∠A=90 ,AB=AC,∠ABD=∠CBD。 求证:BC=AB+AD 例3. 已知如图2-3,△ABC的角平分线 BM、CN相交于点 P。求证:∠BAC的平分线也经过点 P。 (三):作角平分线的垂线构造等腰三角形 例1. 已知:如图3-1,∠BAD=∠DAC,AB>AC,CD⊥AD于 D,H是 BC中点。求证:DH=21 (AB-AC) 图 2-1ABCDEF图2-2ABCDE图2-3PABCMNDF图示3-1ABCDHE 例2. 已知:如图3-2,AB=AC,∠BAC=90 ,AD为∠ABC的平分线,CE⊥BE.求证:BD=2CE。 例3.已知:如图3-3在△ABC中,AD、AE分别∠BAC的内、外角平分线,过顶点 B作 BFAD,交 AD的延长线于 F,连结 FC并延长交 AE于 M。 求证:AM=ME。 例4. 已知:如图3-4,在△ABC中,AD平分∠BAC,AD=AB,CM⊥AD交 AD延长线于 M。求证:AM=21 (AB+AC) 图3-2DABEFC图3-3DBEFNACM图3-4nEBADCMF (四)、以角分线上一点做角的另一边的平行线 图4-2图4-1CABCBAFIEDHG 例4 如图,AB>AC, ∠1=∠2,求证:AB-AC>BD-CD。 例5 如图,BC>BA,BD平分∠ABC,且 AD=CD,求证:∠A+∠C=180。 例6 如图,AB∥CD,AE、DE分别平分∠BAD各∠ADE,求证:AD=AB+CD。 1 2 A C D B B D C A A B E C D 练习: 1. 已知,如图,∠C=2∠A,AC=2BC。求证:△ABC是直角三角形。 2.已知:如图,AB=2AC,∠1=∠2,DA=DB,求证:DC⊥AC 3.已知CE、AD是△ABC的角平分线,∠B=60°,求证:AC=AE+CD 4.已知:如图在△ABC中,∠A=90°,AB=AC,BD是∠ABC的平分线,求证:BC=AB+AD C A B A B C D A E B D C A B D C 1 2 二、 由线段和差想到的辅助线 例1、 已知如图1-1:D、E为△ABC 内两点,求证:AB+AC>BD+DE+CE. 例如:如图2-1:已知D 为△ABC 内的任一...