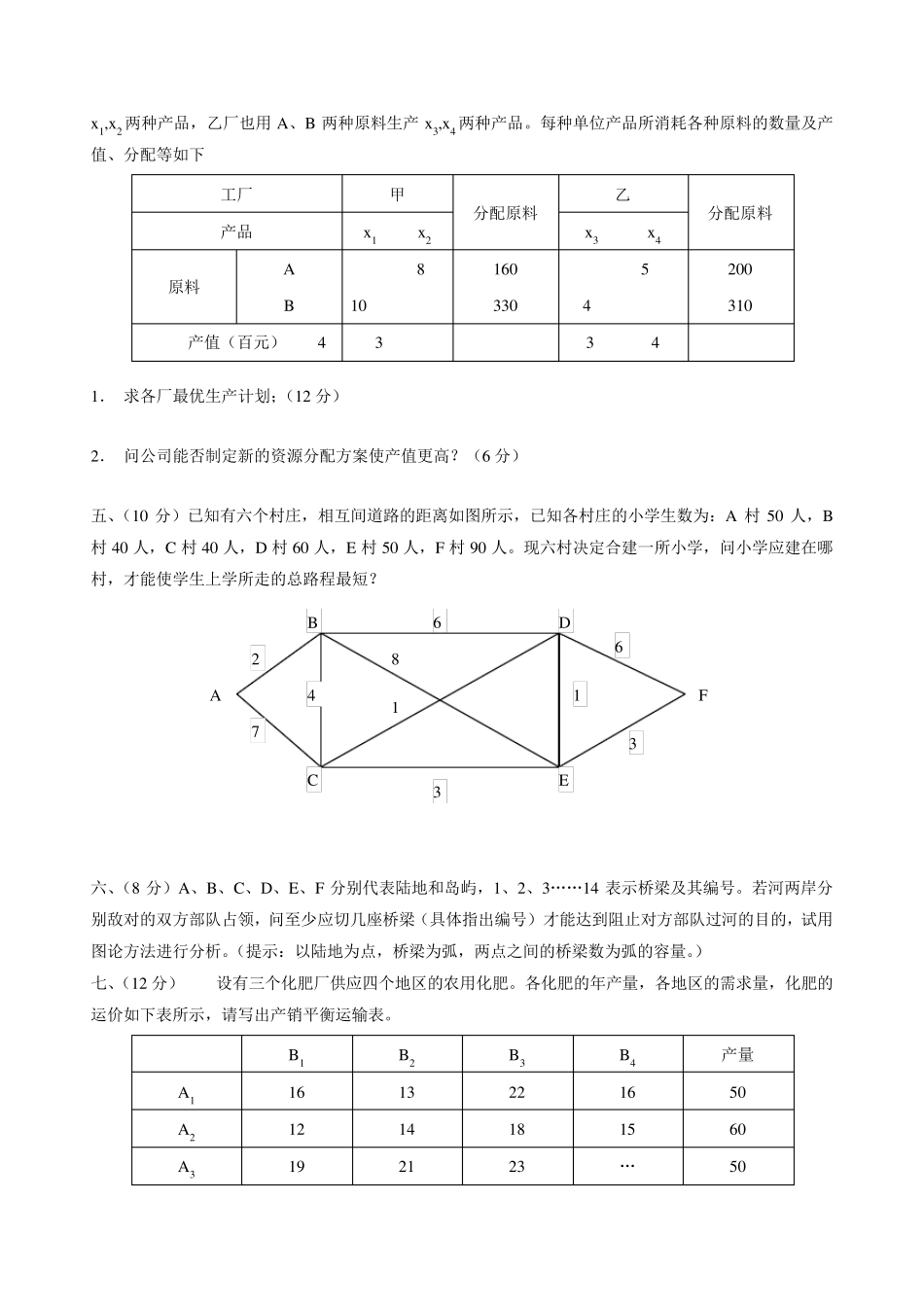
运筹学试卷(1 ) 一、回答下面问题(每小题 3 分) 1. 在 单 纯 形 法 计 算 中 , 如 果 不 按 最 小 比 值 规 则 确 定 换 基 变 量 , 则 在 下 一 个 解 中 一 定 会 出现 。 2. 原问题无界时,其对偶问题 ,反之,当对偶问题无可行解时,原问题 。 3.已知 y0 为线性规划的对偶问题的最优解,若 y0>0,说明在最优生产计划中对应的资源 。 4.已知 y0 为线性规划的对偶问题的最优解,若 y0=0,说明在最优生产计划中对应的资源 。 5.已知线形规划问题的原问题有无穷多最优解,则其对偶问题的最优解一定是 。 6.m 个产地 n 个销地的产销平衡运输问题的模型其决策变量的个数是 个;基变量的个数是 个;决策变量的系数列向量的特点是 。 7.用位势法求解运输问题,位势的含义是 ;行位势与列位势中有一个的取值是任意的,这是因为 。 8.用割平面法求解整数规划,割平面割去了 ;但未割去 。 9.按教材中的符号写出最大流问题的数学模型 。 10.什么是截集,何谓最小截集? 二、(10 分)下表是用单纯形法计算到某一步的表格,已知该线性规划的目标函数值为 z=14 表1 cj x1 x2 x3 x4 x3 x1 2 a c d 0 e 1 0 1/5 1 σj b -1 f g (1) 求 a—g 的值;(8 分) (2) 表中给出的解是否为最优解。(2 分) 三、(每小题 6 分共12 分)车间为全厂生产一种零件,其生产准备费是 100 元,存贮费是 0.05 元/天·个,需求量为每天30 个,而且要保证供应。 1 设车间生产所需零件的时间很短(即看成瞬时供应);2 设车间生产零件的生产率是 50 个/天。 要求在(1)(2)条件下的最优生产批量 Q*,生产间隔期 t*和每天的总费用 C*。 四、(18 分) 某公司下属甲、乙两个厂,有 A 原料 360 斤,B 原料 640 斤。甲厂用 A、B 两种原料生产x1,x2 两种产品,乙厂也用A、B 两种原料生产x3,x4 两种产品。每种单位产品所消耗各种原料的数量及产值、分配等如下 工厂 甲 分配原料 乙 分配原料 产品 x1 x2 x3 x4 原料 A B 8 10 160 330 5 4 200 310 产值(百元) 4 3 3 4 1. 求各厂最优生产计划;(12 分) 2. 问公司能否制定新的资源分配方案使产值更高?(6 分) 五、(10 分)已知有六个村庄,相互间道路的距离如图所示,已知各村庄的小学生数为:A 村50 人,B村40 人,C 村4...