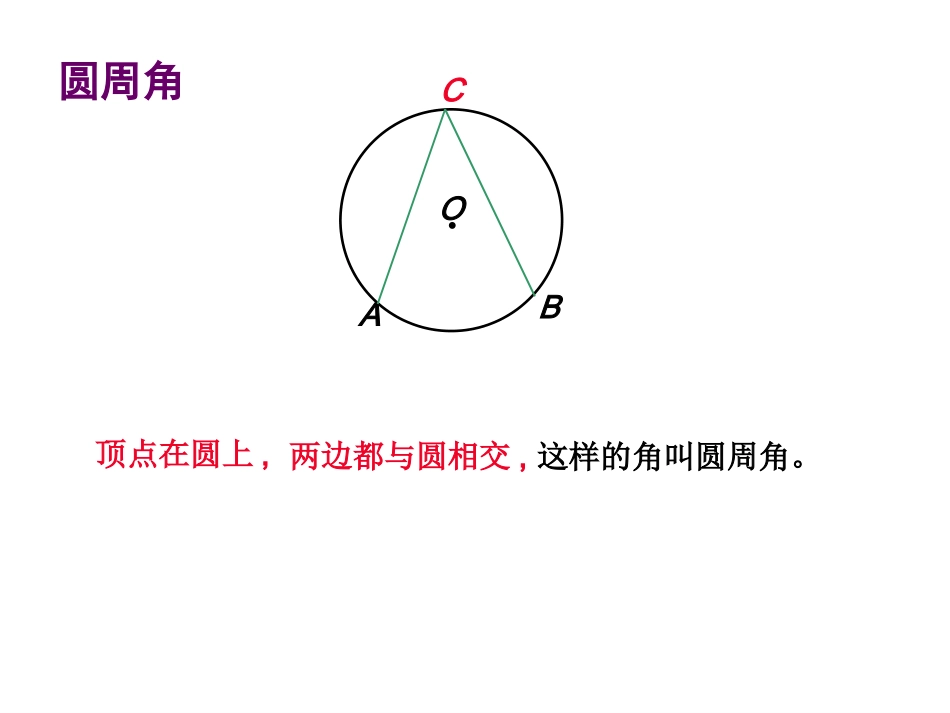
24.1.4圆周角回忆1.什么叫圆心角?.OAB顶点在圆心的角叫圆心角2.圆心角、弧、弦的关系定理是什么?在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。.OA圆周角C顶点在圆上,两边都与圆相交,这样的角叫圆周角。B问题探讨:判断下列图形中所画的∠P是否为圆周角?并说明理由。PPPP不是是不是不是顶点不在圆上。顶点在圆上,两边和圆相交。两边不和圆相交。有一边和圆不相交。•当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?.BACDEE●OBDCAAC所对角∠AEC,∠ABC,∠ADC的大小有什么关系?⌒生活实践•如图,测量圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?你能证明这种关系吗?ABCOABCOABCO1.第一种情况:ABCO∵OA=OC∴∠A=C∠又∠BOC=A∠+∠C∴∠BOC=2A∠∠即A=BOC∠21圆周角∠BAC与圆心角∠BOC的大小关系.ABCOD证明:由第1种情况得∠即BAC=BOC∠21∠BAD=∠BOD21∠CAD=∠COD21∠BAD+∠CAD=∠BOD+∠COD21212.第二种情况:证明:作射线AO交⊙O于D。由第1种情况得∠即BAC=BOC∠21∠BAD=∠BOD21∠CAD=∠COD21∠CAD-∠BAD=∠COD-∠BOD2121ABCOD3.第三种情况:·ABC1OC2C3归纳总结在同圆或等圆中,同弧(或等弧)所对的圆周角相等;都等于这条弧所对的圆心角的一半.圆周角定理直径(或半圆)所对的圆周角是直角,90°的圆周角所对的弦是直径.推论·ABCDEO•当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?.BACDE生活实践E●OBDCA规律:都相等,都等于圆心角∠AOC的一半AC所对的圆周角∠AEC∠ABC∠ADC的大小有什么关系?⌒结论:同弧或等弧所对的圆周角相等。1、如图,在⊙O中,ABC=50°,则∠AOC等于()A、50°;B、80°;C、90°;D、100°ACBOD2、如图,△ABC是等边三角形,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC等于()A、30°;B、60°;C、90°;D、45°CABPB练习练习::3、求圆中角X的度数BAO.70°xAO.X120°练习练习::600BP(1)(2)1200350PDBOAC例:如图,AB是⊙O的直径AB=10cm,弦AC=6cm,ACB∠的平分线交⊙O于点D.求BC,AD,BD的长.1064、如图,△ABC的顶点A、B、C都在⊙O上,∠C=30°,AB=2,则⊙O的半径是。CABO解:连接OA、OB∵∠C=30°,∴∠AOB=60°又∵OA=OB,∴△AOB是等边三角形∴OA=OB=AB=2,即半径为2。2练习练习::5:已知⊙O中弦AB的等于半径,求弦AB所对的圆心角和圆周角的度数。OAB圆心角为60度圆周角为30度或150度。6.试找出下图中所有相等的圆周角。ABCD12345678∠2=7∠∠1=4∠∠3=6∠∠5=8∠7.练习:如图AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.ABOCD40°在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等吗?为什么?在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等.8.如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.DABCOOO·方法一方法二方法三方法四AB使用帮助1.1.圆周角定义圆周角定义::顶点在圆上顶点在圆上,,并且并且两边都和圆两边都和圆相交相交的角叫圆周角的角叫圆周角..3.3.在同圆或等圆中,同弧(或等弧)所对的圆周角相等;都等于这条弧所对的圆心角的一半.;相等;相等的圆周角所对的弧相等。的圆周角所对的弧相等。2.2.半圆或直径所对的圆周角等于半圆或直径所对的圆周角等于90°90°90°90°的圆周角所对的弦是直径的圆周角所对的弦是直径小结小结::