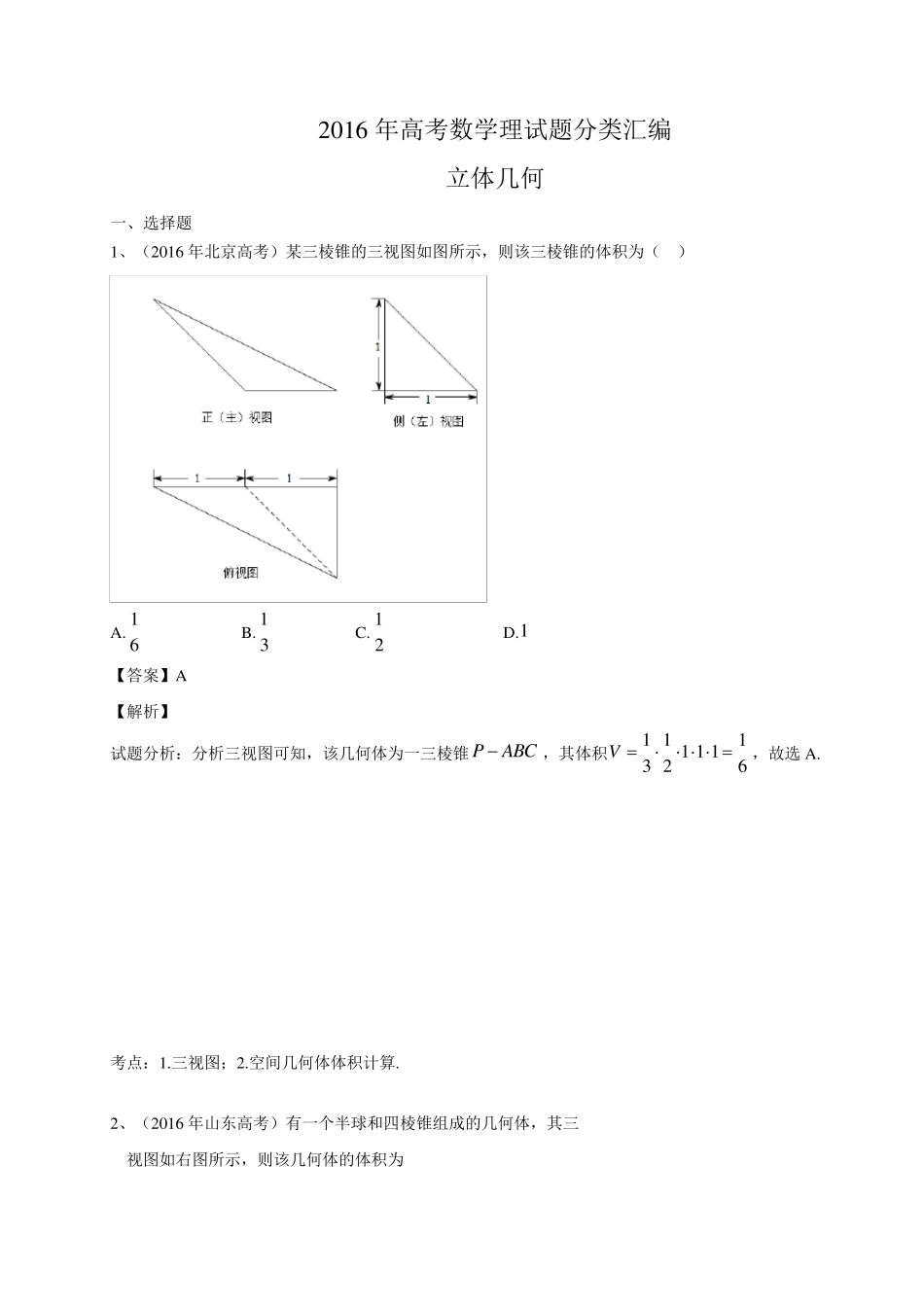
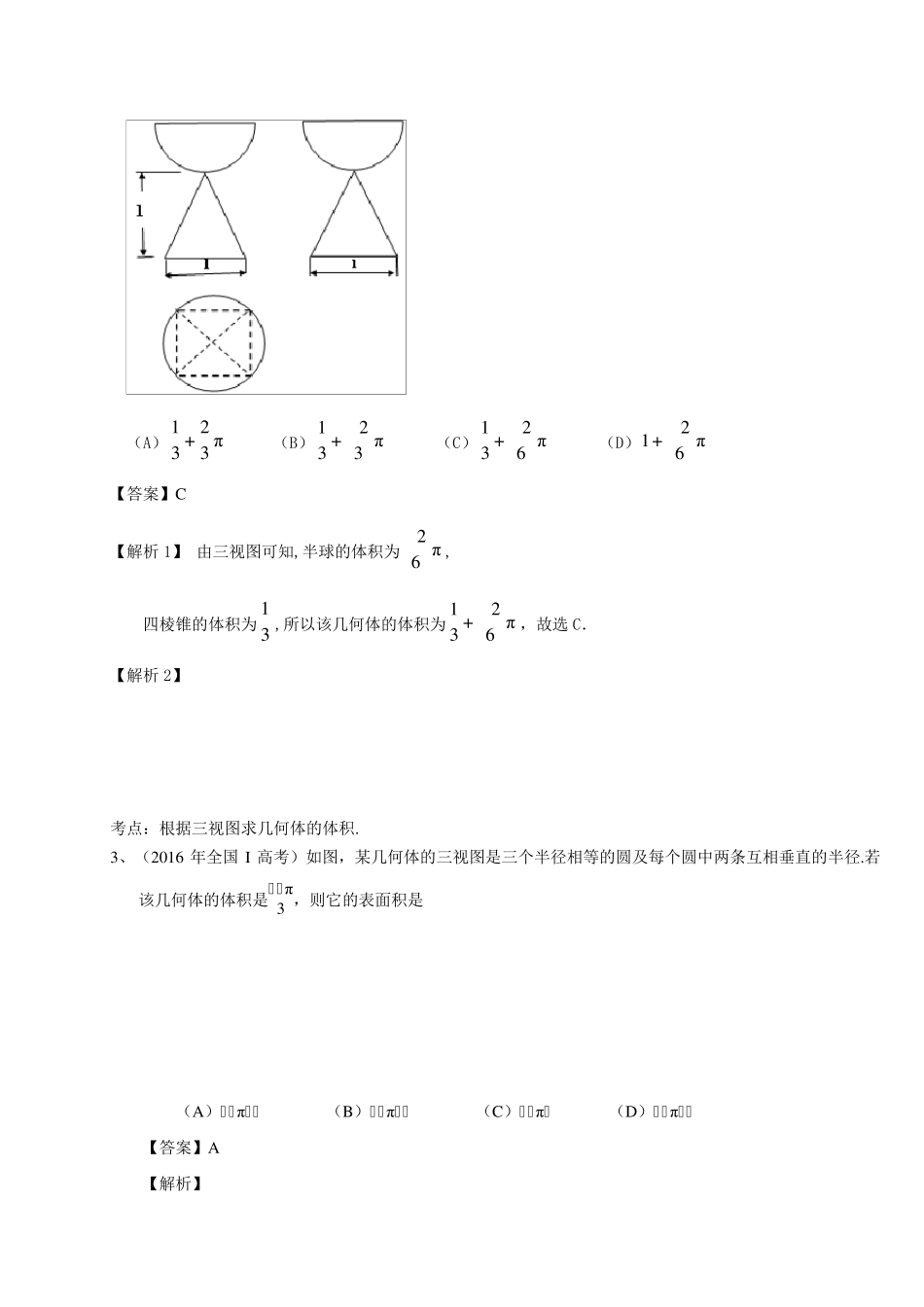
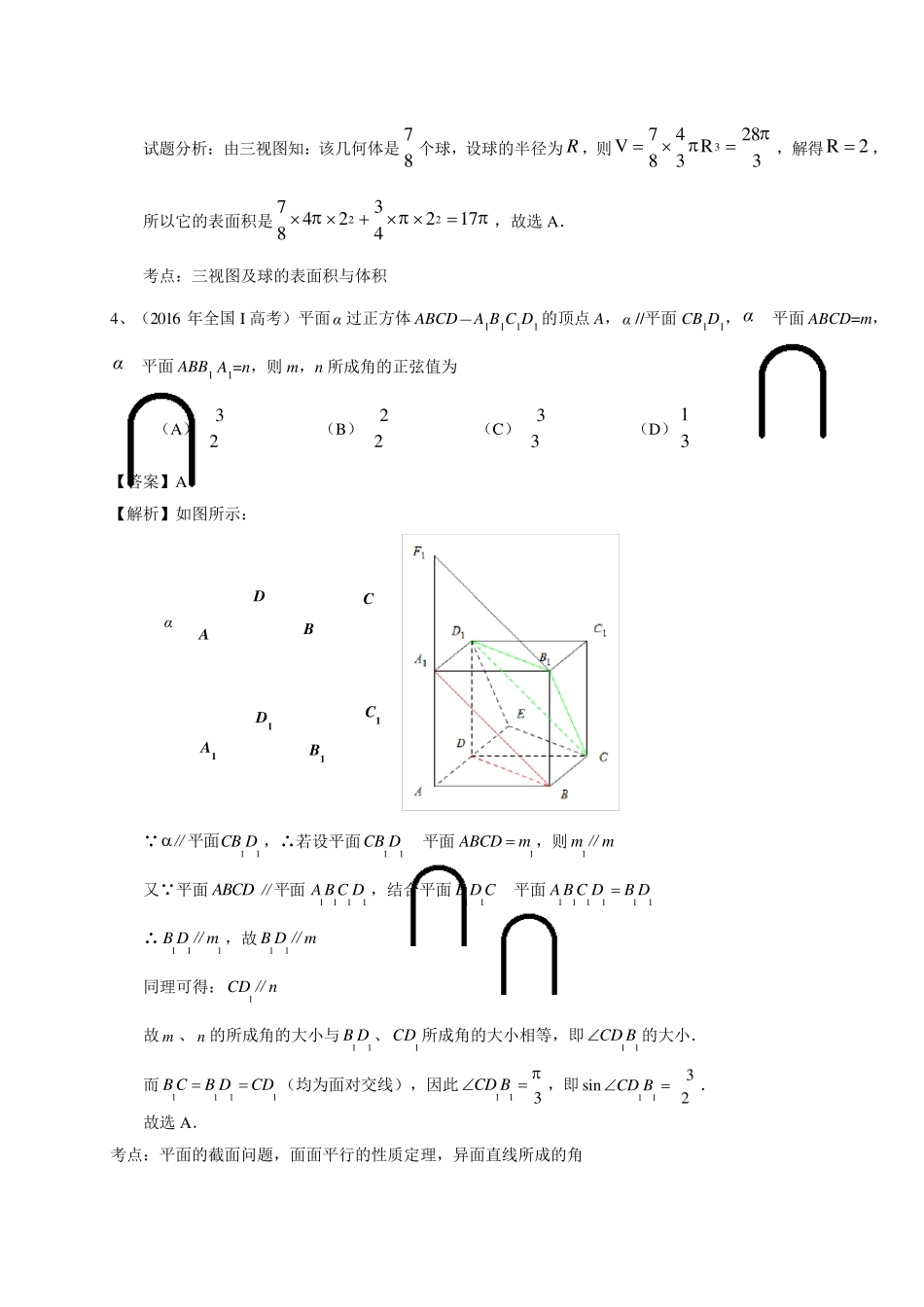
2016 年高考数学理试题分类汇编 立体几何 一、选择题 1、(2016 年北京高考)某三棱锥的三视图如图所示,则该三棱锥的体积为( ) A. 16 B. 13 C. 12 D.1 【答案】A 【解析】 试题分析:分析三视图可知,该几何体为一三棱锥 PABC,其体积1 111 1 13 26V ,故选 A. 考点:1.三视图;2.空间几何体体积计算. 2、(2016 年山东高考)有一个半球和四棱锥组成的几何体,其三 视图如右图所示,则该几何体的体积为 (A)π32+31 (B) π32+31 (C) π62+31 (D) π62+1 【答案】C 【解析1】 由三视图可知,半球的体积为π62, 四棱锥的体积为31,所以该几何体的体积为 π62+31,故选C. 【解析2】 考点:根据三视图求几何体的体积. 3、(2016 年全国 I高考)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3 ,则它的表面积是 (A)17π (B)18π (C)20π (D)28π 【答案】A 【解析】 试题分析:由三视图知:该几何体是78 个球,设球的半径为R ,则37428VR833,解得R2,所以它的表面积是22734221784,故选A. 考点:三视图及球的表面积与体积 4、(2016 年全国I 高考)平面α 过正方体ABCDA1B1C1D1 的顶点A,α //平面CB1D1,α平面ABCD=m,α平面ABB1 A1=n,则m,n所成角的正弦值为 (A)32 (B)22 (C)33 (D)13 【答案】A 【解析】如图所示: αAA1BB1DCC1D1 11CB D∥平面,∴若设平面11CB D平面1ABCDm,则1mm∥ 又 平面ABCD ∥平面1111A BC D ,结合平面11B D C平面111111A B C DB D ∴111B Dm∥,故11B Dm∥ 同理可得:1CDn∥ 故m 、n的所成角的大小与11B D 、1CD 所成角的大小相等,即11CD B的大小. 而1111B CB DCD(均为面对交线),因此113CD B,即113sin2CD B. 故选A. 考点:平面的截面问题,面面平行的性质定理,异面直线所成的角 5、(2016 年全国 II高考)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为 (A)20π (B)24π (C)28π (D)32π 【答案】C 【解析】C 几何体是圆锥与圆柱的组合体, 设圆柱底面圆半径为 r ,周长为 c ,圆锥母线长为l ,圆柱高为 h . 由图得2r ,2π4πcr,由勾股定理得:2222 34l , 21π2Srch...