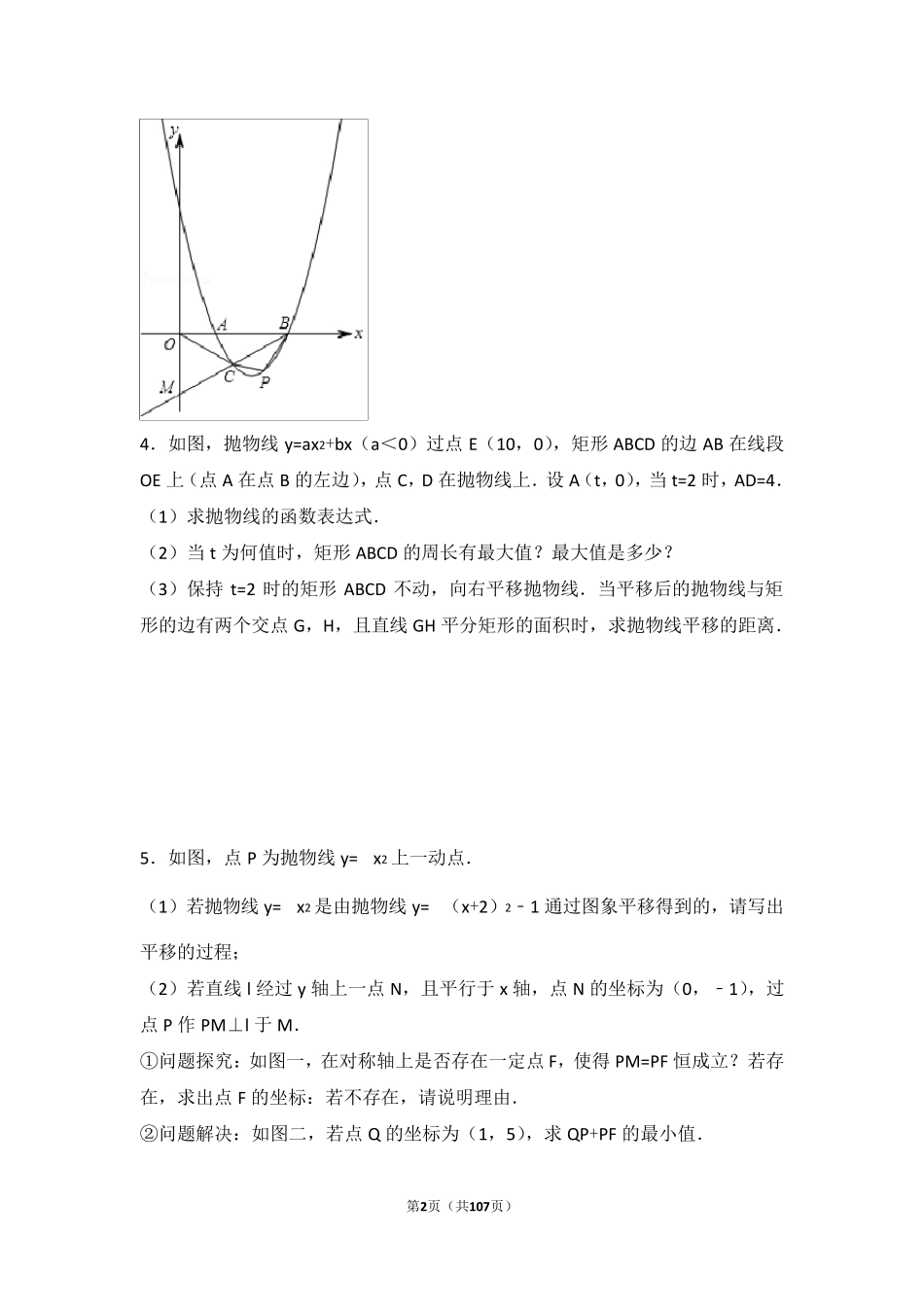
第1页(共107页) 2018 年中考二次函数压轴题汇编 2.如图1,已知抛物线y=﹣x2+bx+c 与x 轴交于A(﹣1,0),B(3,0)两点,与y 轴交于C 点,点P 是抛物线上在第一象限内的一个动点,且点P 的横坐标为t. (1)求抛物线的表达式; (2)设抛物线的对称轴为l,l 与x 轴的交点为D.在直线l 上是否存在点M,使得四边形CDPM 是平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由. (3)如图2,连接BC,PB,PC,设△PBC 的面积为S. ①求S 关于t 的函数表达式; ②求P 点到直线BC 的距离的最大值,并求出此时点P 的坐标. 3.如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x 轴交于A、B 两点,抛物线上另有一点C 在x 轴下方,且使△OCA∽△OBC. (1)求线段 OC 的长度; (2)设直线BC 与y 轴交于点M,点C 是BM 的中点时,求直线BM 和抛物线的解析式; (3)在(2)的条件下,直线BC 下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P 的坐标;若不存在,请说明理由. 第2页(共107页) 4.如图,抛物线y=ax2+bx(a<0)过点E(10,0),矩形ABCD 的边AB 在线段OE 上(点A 在点B 的左边),点C,D 在抛物线上.设A(t,0),当t=2 时,AD=4. (1)求抛物线的函数表达式. (2)当t 为何值时,矩形ABCD 的周长有最大值?最大值是多少? (3)保持t=2 时的矩形ABCD 不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH 平分矩形的面积时,求抛物线平移的距离. 5.如图,点P 为抛物线y=x2 上一动点. (1)若抛物线y=x2 是由抛物线y= (x+2)2﹣1 通过图象平移得到的,请写出平移的过程; (2)若直线l 经过y 轴上一点N,且平行于x 轴,点N 的坐标为(0,﹣1),过点P 作PM⊥l 于M. ①问题探究:如图一,在对称轴上是否存在一定点F,使得PM=PF 恒成立?若存在,求出点F 的坐标:若不存在,请说明理由. ②问题解决:如图二,若点Q 的坐标为(1,5),求QP+PF 的最小值. 第3页(共107页) 6.已知直线y=x+3 与x 轴、y 轴分别相交于A、B 两点,抛物线y=x2+bx+c 经过A、B 两点,点M 在线段OA 上,从O 点出发,向点A 以每秒1 个单位的速度匀速运动;同时点N 在线段AB 上,从点A 出发,向点B 以每秒个单位的速度匀速运动,连接MN,设运动时间为t 秒 (1)求抛物线解析式; (2)当t 为何值时,...