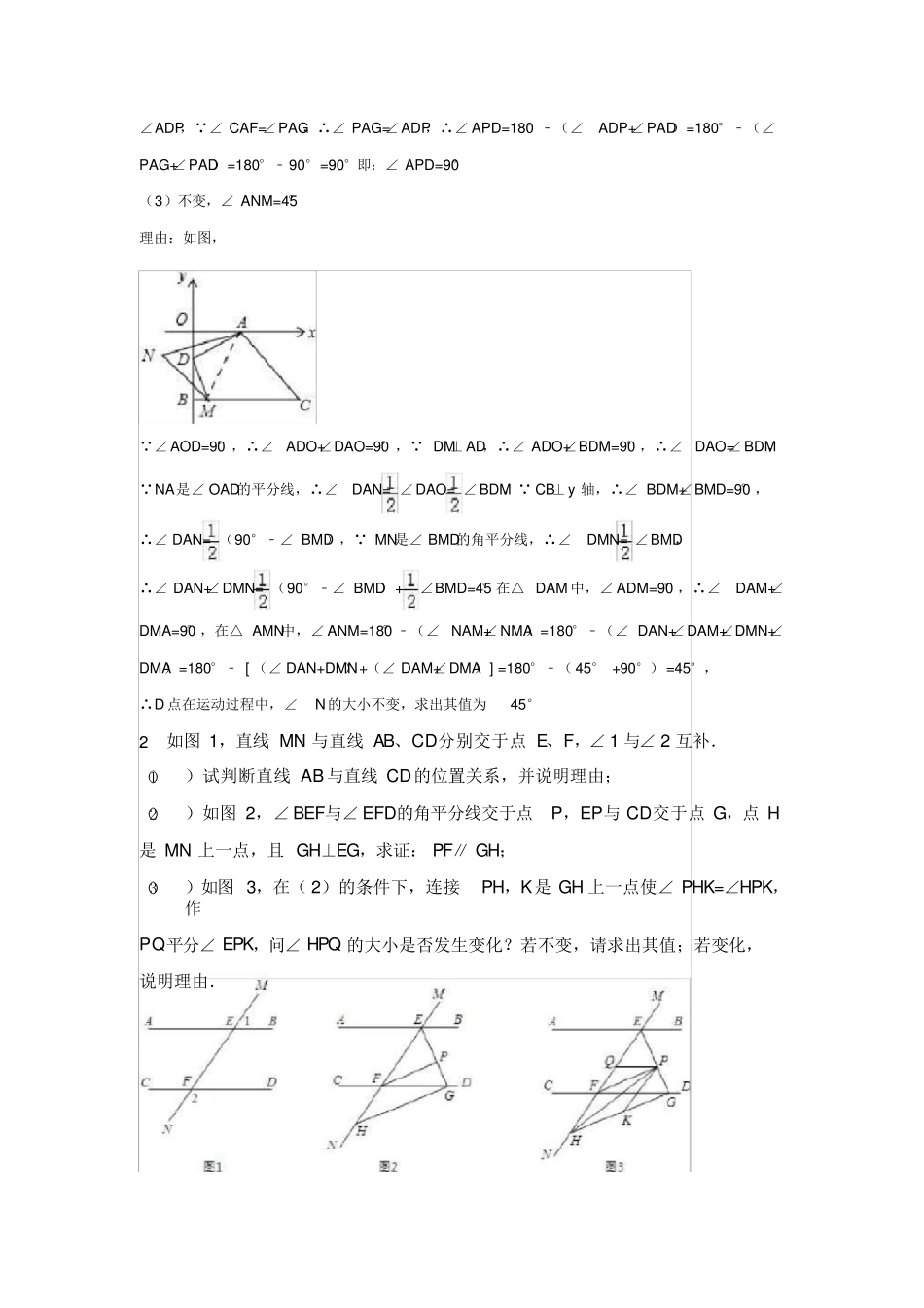
2 七年级下册动点问题及压轴题 1.如图 1,在平面直角坐标系中, A(a,0)是 x 轴正半轴上一点, C是第四象限一点, CB⊥y 轴,交 y 轴负半轴于 B(0,b),且( a﹣3) +|b+4|=0 ,S 四边形 AOBC=1.6 (1) )求 C点坐标; (2) )如图 2,设 D为线段 OB上一动点, 当 AD⊥AC时,∠ODA的角平分线与∠ CAE 的角平分线的反向延长线交于点 P,求∠ APD的度数. (3) )如图 3,当 D点在线段 OB上运动时,作 DM⊥AD交 BC于 M点,∠ BMD、∠ DAO的平分线交于 N点,则 D点在运动过程中,∠ N的大小是否变化?若不变,求出其值,若变化,说明理由. 【解答】解:( 1) ( a﹣3) 2+|b+4|=0 , ∴ a﹣ 3=0, b+4=0, ∴a=3, b=﹣ 4, ∴ A( 3,0), B(0,﹣ 4), ∴ OA=3, OB=4, S 四边形 AOBC=16. ∴ (OA+BC)× OB=16, ∴ ( 3+BC)× 4=16, ∴ BC=5, C 是第四象限一点, CB⊥ y 轴, ∴ C( 5,﹣ 4) (2)如图, 延长 CA, AF 是∠ CAE的角平分线, ∴∠ CAF= ∠ CAE, ∠ CAE=∠ OAG,∴∠ CAF= ∠ OAG, AD⊥ AC,∴∠ DAO+∠ OAG=∠PAD+∠PAG=9°0 , ∠ AOD=9°0 ,∴∠ DAO+∠ADO=9°0 , ∴∠ ADO=∠ OAG,∴∠ CAF= ∠ADO, DP 是∠ ODA的角平分线∴∠ ADO=2∠ ADP,∴∠ CAF= ∠ADP, ∠ CAF=∠ PAG,∴∠ PAG=∠ ADP,∴∠ APD=18°0 ﹣(∠ ADP+∠ PAD)=180°﹣(∠ PAG+∠ PAD)=180°﹣ 90°=90°即:∠ APD=90° (3)不变,∠ ANM=4°5 理由:如图, ∠ AOD=9°0 ,∴∠ ADO+∠DAO=9°0 , DM⊥ AD,∴∠ ADO+∠BDM=9°0 ,∴∠ DAO=∠ BDM, NA是∠ OAD的平分线,∴∠ DAN= ∠ DAO= ∠ BDM, CB⊥ y 轴,∴∠ BDM∠+ BMD=9°0 , ∴∠ DAN= (90°﹣∠ BMD), MN是∠ BMD的角平分线,∴∠ DMN= ∠ BMD, ∴∠ DAN+∠ DMN= (90°﹣∠ BMD) + ∠BMD=4°5 在△ DAM 中,∠ ADM=9°0 ,∴∠ DAM+∠ DMA=9°0 ,在△ AMN中,∠ ANM=18°0 ﹣(∠ NAM∠+ NMA)=180°﹣(∠ DAN+∠ DAM+∠DMN+∠ DMA)=180°﹣ [ (∠ DAN+DM)N +(∠ DAM∠+ DMA) ] =180°﹣( 45° +90°) =45°, ∴D 点在运动过程中,∠ N 的大小不变,求出其值为 45° 2. 如图 1,直线 MN ...