matlab实现DFTVIP免费

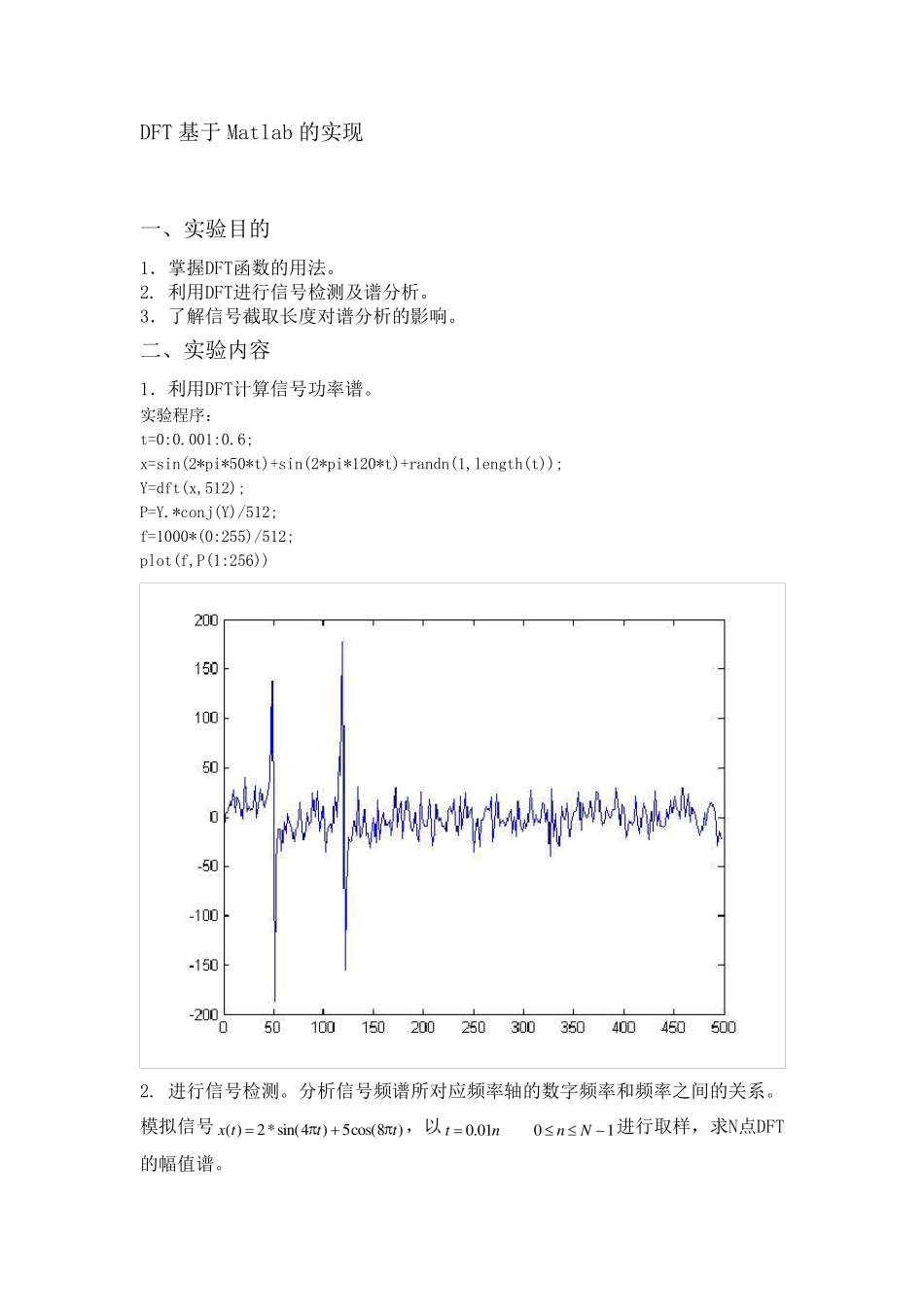
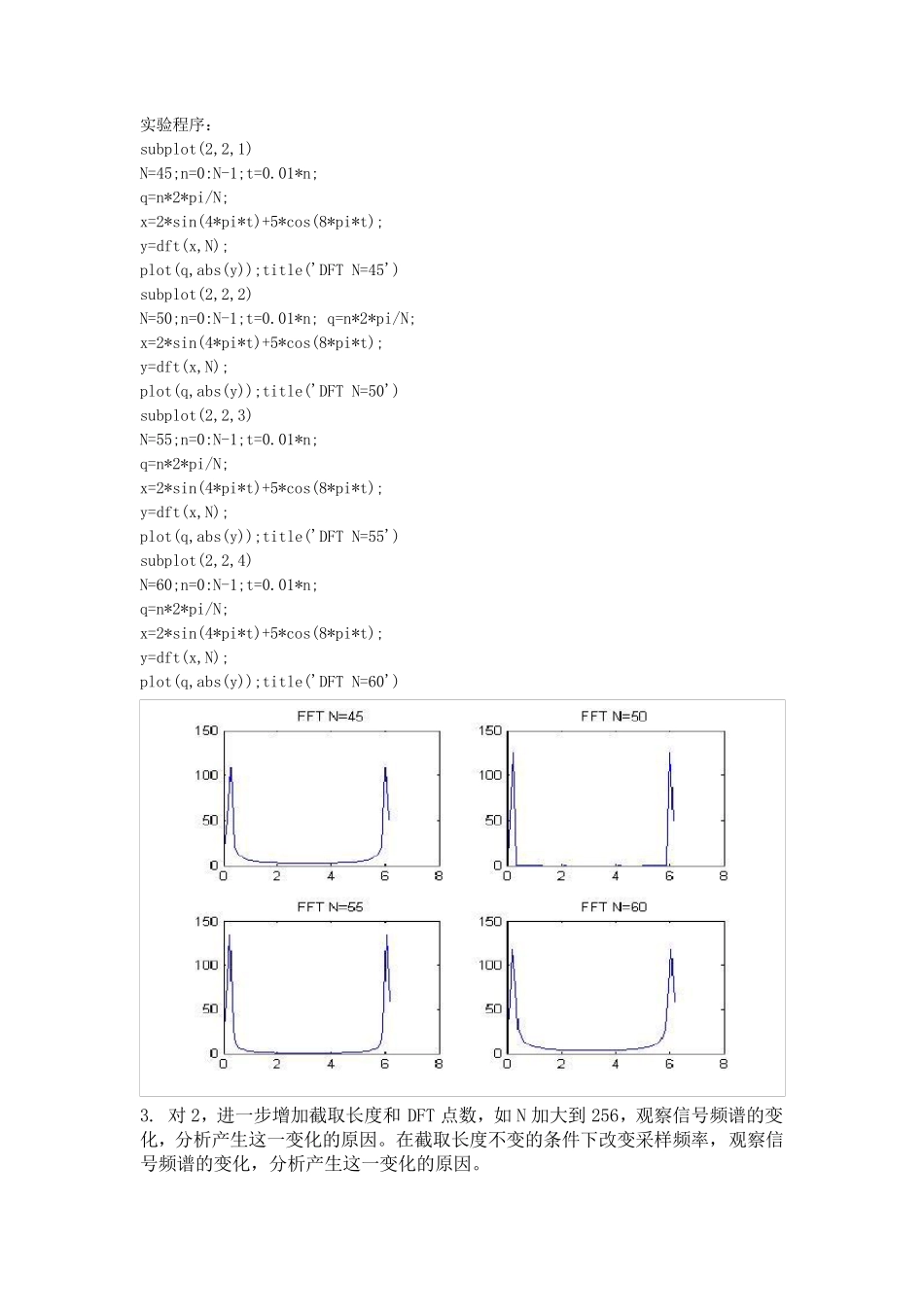
DFT 基于Matlab 的实现 一、实验目的 1．掌握DFT函数的用法。 2. 利用DFT进行信号检测及谱分析。 3．了解信号截取长度对谱分析的影响。 二、实验内容 1．利用DFT计算信号功率谱。 实验程序： t=0:0.001:0.6; x=sin(2*pi*50*t)+sin(2*pi*120*t)+randn(1,length(t)); Y=dft(x,512); P=Y.*conj(Y)/512; f=1000*(0:255)/512; plot(f,P(1:256)) 2. 进行信号检测。分析信号频谱所对应频率轴的数字频率和频率之间的关系。模拟信号)8cos(5)4sin(*2)(tttx，以nt01.0 10Nn进行取样，求N点DFT的幅值谱。 实验程序： subplot(2,2,1) N=45;n=0:N-1;t=0.01*n; q=n*2*pi/N; x=2*sin(4*pi*t)+5*cos(8*pi*t); y=dft(x,N); plot(q,abs(y));title('DFT N=45') subplot(2,2,2) N=50;n=0:N-1;t=0.01*n; q=n*2*pi/N; x=2*sin(4*pi*t)+5*cos(8*pi*t); y=dft(x,N); plot(q,abs(y));title('DFT N=50') subplot(2,2,3) N=55;n=0:N-1;t=0.01*n; q=n*2*pi/N; x=2*sin(4*pi*t)+5*cos(8*pi*t); y=dft(x,N); plot(q,abs(y));title('DFT N=55') subplot(2,2,4) N=60;n=0:N-1;t=0.01*n; q=n*2*pi/N; x=2*sin(4*pi*t)+5*cos(8*pi*t); y=dft(x,N); plot(q,abs(y));title('DFT N=60') 3. 对2，进一步增加截取长度和DFT 点数，如N 加大到256，观察信号频谱的变化，分析产生这一变化的原因。在截取长度不变的条件下改变采样频率，观察信号频谱的变化，分析产生这一变化的原因。 N加大到256时的程序： N=256;n=0:N-1;t=0.01*n; q=n*2*pi/N; x=2*sin(4*pi*t)+5*cos(8*pi*t); y=dft(x,N); plot(q,abs(y));title('DFT N=256') 分析原因：在T=0.01s 的情况下，第一个序列的周期是100，第二个序列的周期是50，所以当取样点数小于100 时，频率分辨率不够，不能够区分出两个信号。当采样点数足够多（256）时，频率分辨率增加，能够区分出两个频率的信号。 将采样间隔变为 T=0.1s 时，N 仍为 45 的程序： N=45;n=0:N-1;t=0.1*n; q=n*2*pi/N; x=2*sin(4*pi*t)+5*cos(8*pi*t); y=dft(x,N); plot(q,abs(y));title('DFT N=45') 分析原因：在T=0. 1s 的情况下，第一个序列的周期是10，第二个序列的周期是5，所以当取样点数为45 时，能够区分出两个信号。 参数同上，N 取64，并在信号中加入噪声 w(t)。 figure(2) subplot(2,1,1) N=64;n=0:N-1;t=0.01*n; q=n*2*pi/N; x=2*sin(4*pi*t)+5*cos(8*pi...