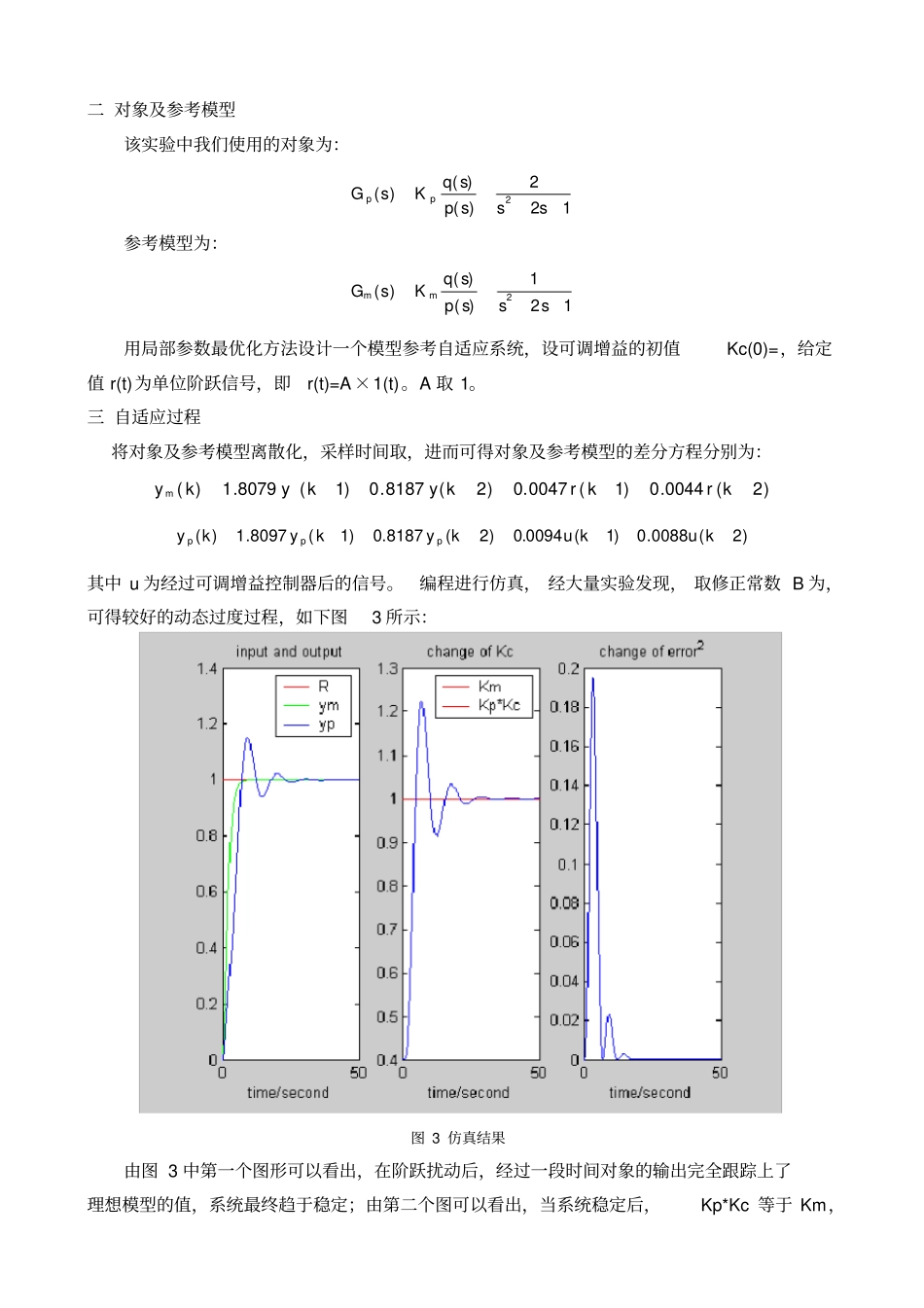
一 原理及方法模型参考自适应系统,是用理想模型代表过程期望的动态特征,可使被控系统的特征与理想模型相一致。一般模型参考自适应控制系统的结构如图1 所示。图 1 一般的模型参考自适应控制系统其工作原理为,当外界条件发生变化或出现干扰时,被控对象的特征也会产生相应的变化,通过检测出实际系统与理想模型之间的误差,由自适应机构对可调系统的参数进行调整,补偿外界环境或其他干扰对系统的影响,逐步使性能指标达到最小值。基于这种结构的模型参考自适应控制有很多种方案,其中由麻省理工学院科研人员首先利用局部参数最优化方法设计出世界上第一个真正意义上的自适应控制律,简称为 MIT 自适应控制,其结构如图2 所示。图 2 MIT 控制结构图系统中, 理想模型 Km 为常数,由期望动态特性所得, 被控系统中的增益Kp 在外界环境发生变化或有其他干扰出现时可能会受到影响而产生变化,从而使其动态特征发生偏离。而Kp 的变化是不可测量的,但这种特性的变化会体现在广义误差e 上,为了消除或降低由于Kp 的变化造成的影响, 在系统中增加一个可调增益Kc,来补偿 Kp 的变化,自适应机构的任务即是依据误差最小指标及时调整Kc,使得 Kc 与 Kp 的乘积始终与理想的Km 一致,这里使用的优化方法为最优梯度法,自适应律为:tmdyeBKctKc0)0()(MIT 方法的优点在于理论简单,实施方便,动态过程总偏差小,偏差消除的速率快,而且用模拟元件就可以实现;缺点是不能保证过程的稳定性,换言之,被控对象可能会发散。YpYme+__+R参 考 模 型调 节 器被 控 对 象适 应 机 构可调系统— — —kmq(s)p(s)KcKpq(s)-----p(s)适 应 律Rymype+-二 对象及参考模型该实验中我们使用的对象为:122)()()(2ssspsqKsGpp参考模型为:121)()()(2ssspsqKsGmm用局部参数最优化方法设计一个模型参考自适应系统,设可调增益的初值Kc(0)=,给定值 r(t)为单位阶跃信号,即r(t)=A×1(t)。A 取 1。三 自适应过程将对象及参考模型离散化,采样时间取,进而可得对象及参考模型的差分方程分别为:)2(0044.0)1(0047.0)2(8187.0)1(8079.1)(krkrkykyky m)2(0088.0)1(0094.0)2(8187.0)1(8097.1)(kukukykykyppp其中 u 为经过可调增益控制器后的信号。编程进行仿真, 经大量实验发现, 取修正常数 B 为,可得较好的动态过度过程,如下图3 所示:图 3 仿真结果由图 3 中第一个图形可以看出,在阶跃扰动后,经过一段时间对象的输出...