《固体物理学》房晓勇习题01第一章晶体的结构VIP免费

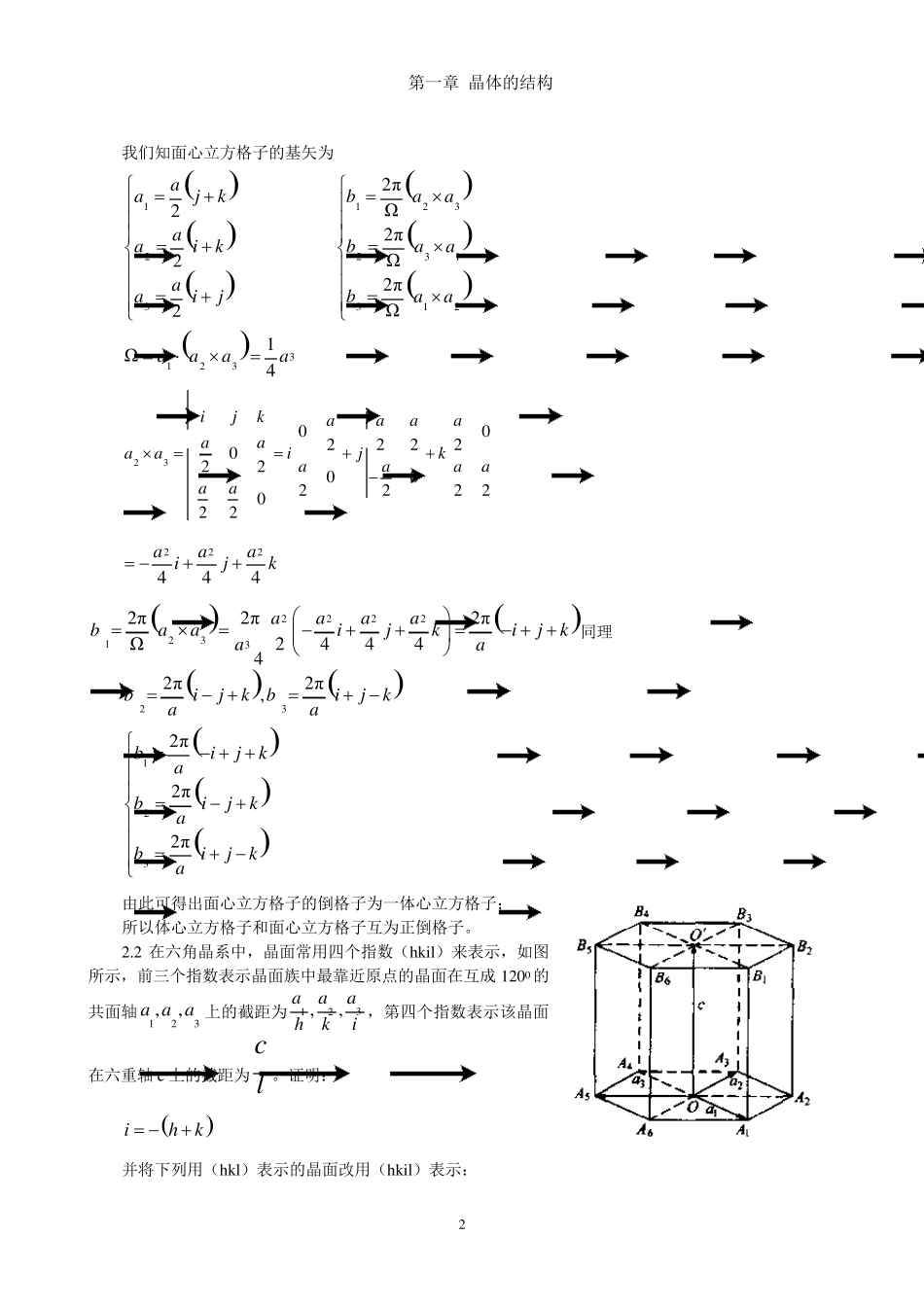
第一章 晶体的结构 1 第一章 晶体的结构 1 .1 试证明体心立方格子和面心立方格子互为正倒格子。 解：我们知体心立方格子的基矢为： 123222aaijkaaijkaaijk  根据倒格子基矢的定义，我们很容易可求出体心立方格子的倒格子基矢为： 1232313122 πΩ2 πΩ2 πΩbaabaabaa 31231Ω2aaaa 23222222222222222222ijkaaaaaaaaaaaijkaaaaaaaaa 2222aajk 223132 π2 π2 πΩ22abaajkjkaa 同理 232 π2 π,bikbijaa 1232 π2 π2 πbjkabikabija 由此可知，体心立方格子的倒格子为一面心立方格子。 第一章 晶体的结构 2 我们知面心立方格子的基矢为 123222aajkaaikaaij 1232313122πΩ2πΩ2πΩbaabaabaa 31231Ω4aaaa 23002222022002222022ijkaaaaaaaaijkaaaaaa 222444aaaijk  222223132π2π2πΩ24444aaaabaaijkijkaa 同理 232π2π,bijkbijkaa 1232π2π2πbijkabijkabijka  由此可得出面心立方格子的倒格子为一体心立方格子； 所以体心立方格子和面心立方格子互为正倒格子。 2.2 在六角晶系中，晶面常用四个指数（hkil）来表示，如图所示，前三个指数表示晶面族中最靠近原点的晶面在互成 1200 的共面轴123,,a a a 上的截距为312,, aaahki ，第四个指数表示该晶面在六重轴 c 上的截距为cl 。证明： ihk  并将下列用（hkl）表示的晶面改用（hkil）表示： 第一章 晶体的结构 3        001 , 133 , 110 , 323 , 100 , 010 , 213 . 证明：林鸿生 1.1.4 王矜奉 1.2.3 如图所示，某一晶面 MN 与六角形平面基矢123,,a a a 轴上的截距 ,,,aaaOAn OBn OCnhki  且60 ,120AOBCOBAOC  有()C()()AOBOBAOC面积面积面积 即111sinsinsin222OA OBAOBOC OBCOBOA OCAOC 代入,,,aaaOAn OBn OCnhki...