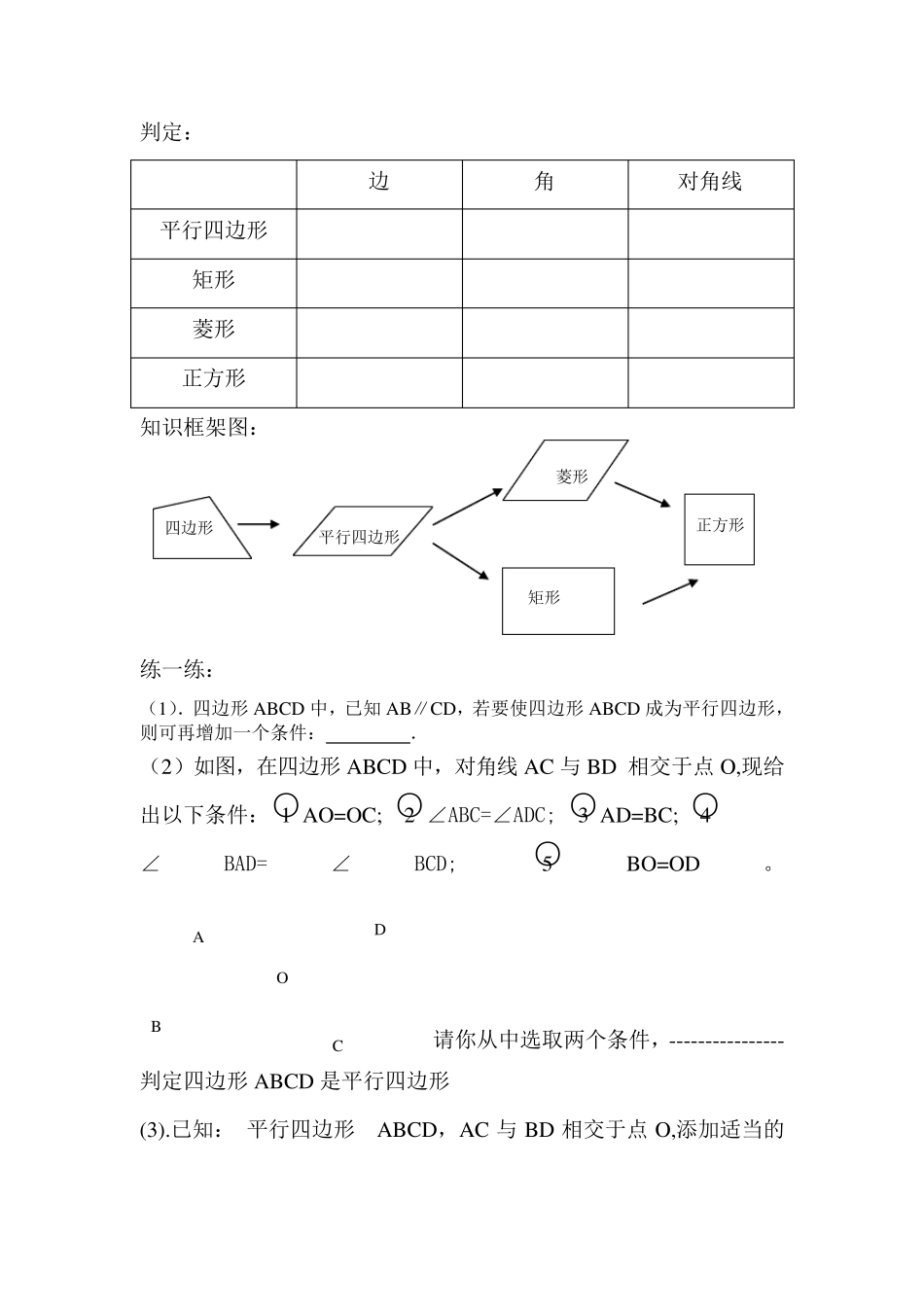
《平行四边形》复习课教学设计 教学内容分析:本课是中考复习课 ,主要内容是平行四边形判定以及特殊的平行四边形——矩形、菱形、正方形的判定及应用。 教学目标: 1 、建立平行四边形及特殊平行四边形的知识框架,掌握平行四边形及特殊平行四边形的判定,并能熟练应用。 2 、经历应用定理解决问题的过程,掌握解决平行四边形问题的一般方法。 3 、运用图形的变换探索图形特征与性质,体会数学研究和发现的过程,领悟知识的生成,发展与变化,发展空间观念。 教学重点:掌握解决平行四边形问题的一般方法,能够从边、角、对角线三个方面思考问题。 教学难点:平行四边形有关知识的综合运用。 教学过程:本节课设计了五个环节,第一个环节——师生共同完成知识框架的建构,第二个环节——解决问题,第三个环节——探究提高,第四个环节——课堂小结,第五个环节——布置作业。 第一个环节:平行四边形的知识系统 教师出示表格,学生完成填空。 判定: 边 角 对角线 平行四边形 矩形 菱形 正方形 知识框架图: 练一练: (1).四边形ABCD 中,已知AB∥CD,若要使四边形ABCD 成为平行四边形,则可再增加一个条件: . (2)如图,在四边形ABCD 中,对角线AC 与BD 相交于点O,现给出以下条件:○1 AO=OC; ○2 ∠ABC=∠ADC; ○3 AD=BC; ○4 ∠BAD=∠BCD; ○5BO=OD。 请你从中选取两个条件,---------------- 判定四边形ABCD 是平行四边形 (3).已知: 平行四边形 ABCD,AC 与BD 相交于点O,添加适当的A B D O 四边形 平行四边形 矩形 菱形 正方形 C 条件 (1)使它成为菱形.条件:______. A (2)使它成为矩形.条件:______. (3)使它成为正方形.条件:_____. B C (4)在四边形ABCD 中,O是对角线的交点,能判定这个四边形是正方形的条件是( ) A. AC=BD, AB∥CD ,AB=CD. B. AD∥BC, ∠BAD=∠BCD. C. AO=BO=CO=DO, AC⊥BD. D. AO=CO, BO=DO, AB=BC. 设计意图:本环节主要是使学生将知识系统化,复习矩形、菱形、正方形判定定理及性质定理,明确平行四边形、矩形、菱形、正方形彼此间的联系。通过学生解决简单的问题,初步回顾定理的应用,激发起学生学习的兴趣和自信心。 第二个环节:解决问题 已知:△ABC 中AB=AC=a,M 为底边BC 上任意一点, 过点M 分别作 AB、AC 的平行线交AB 于 E,交AC 于 F. (1) 四边形AEMF 是平行四边形...