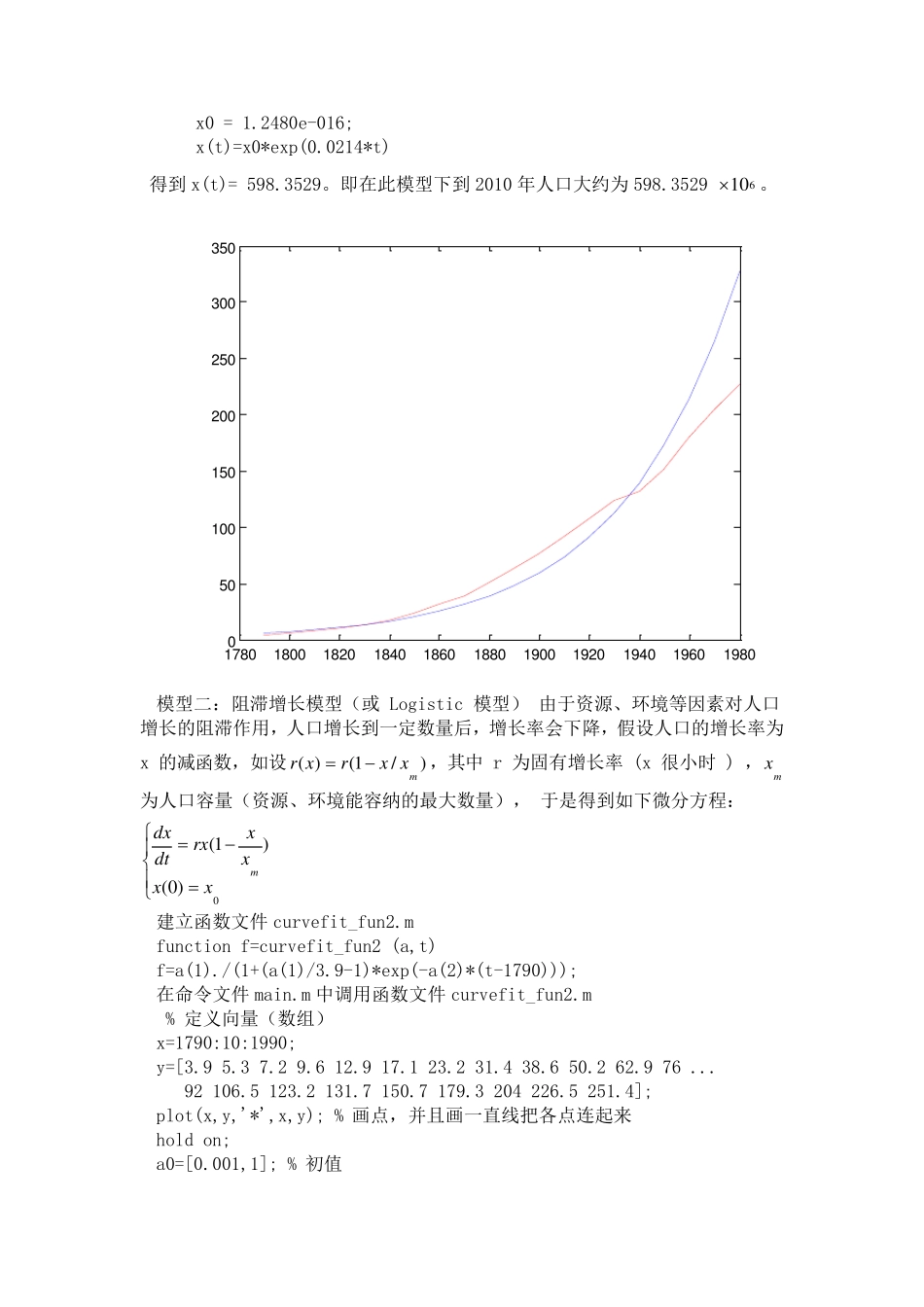
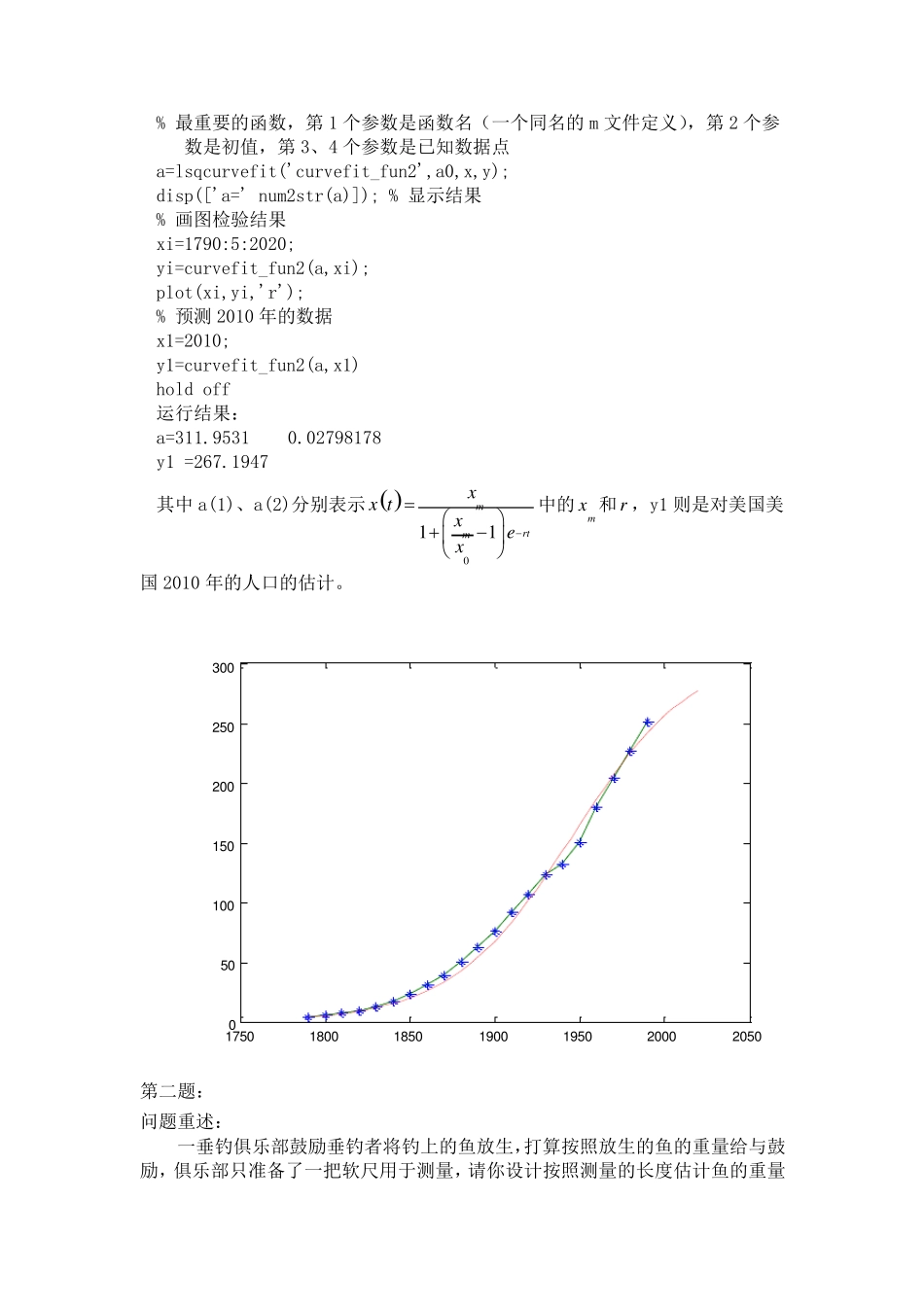
根据美国人口从1790 年到1990 年间的人口数据(如下表),确定人口指数增长模型和Logistic 模型中的待定参数,估计出美国2010 年的人口,同时画出拟合效果的图形。 表1 美国人口统计数据 年 份 1790 1800 1810 1820 1830 1840 1850 人口(×106) 3.9 5.3 7.2 9.6 12.9 17.1 23.2 年 份 1860 1870 1880 1890 1900 1910 1920 人口(×106) 31.4 38.6 50.2 62.9 76.0 92.0 106.5 年 份 1930 1940 1950 1960 1970 1980 人口(×106) 123.2 131.7 150.7 179.3 204.0 226.5 提示: 指数增长模型:rtextx0)( Logistic 模型: 011mrtmxx txex 解:模型一:指数增长模型。Malthus 模型的基本假设下,人口的增长率为常数,记为 r,记时刻 t 的人口为 )(tx,(即)(tx为模型的状态变量)且初始时刻的人口为0x ,因为0)0(xxrxdtdx由假设可知0( )rtx tx e 经拟合得到: 2120010120( )ln( )ln,ln( ),,lnrtaya tax tx ex txrtra xeyx t ar ax 程序: t=1790:10:1980; x(t)=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 ]; y=log(x(t));a=polyfit(t,y,1) r=a(1),x0=exp(a(2)) x1=x0.*exp(r.*t); plot(t,x(t),'r',t,x1,'b') 结果:a = 0.0214 -36.6198 r= 0.0214 x0= 1.2480e-016 所以得到人口关于时间的函数为:0.02140( )tx tx e,其中x0 = 1.2480e-016, 输入:t=2010; x0 = 1.2480e-016; x(t)=x0*exp(0.0214*t) 得到x(t)= 598.3529。即在此模型下到2010 年人口大约为598.3529 61 0。 17801800182018401860188019001920194019601980050100150200250300350 模型二:阻滞增长模型(或 Logistic 模型) 由于资源、环境等因素对人口增长的阻滞作用,人口增长到一定数量后,增长率会下降,假设人口的增长率为 x 的减函数,如设)/1()(mxxrxr,其中 r 为固有增长率 (x 很小时 ) ,mx为人口容量(资源、环境能容纳的最大数量), 于是得到如下微分方程: 0)0()1(xxxxrxdtdxm 建立函数文件 curvefit_fun2.m function f=curvefit_fun2 (a,t) f=a(1)./(1+(a(1)/3.9-1)*exp(-a(2)*(t-1790))); 在命令文件 main.m 中调用函数文件 curvefit_fun2...