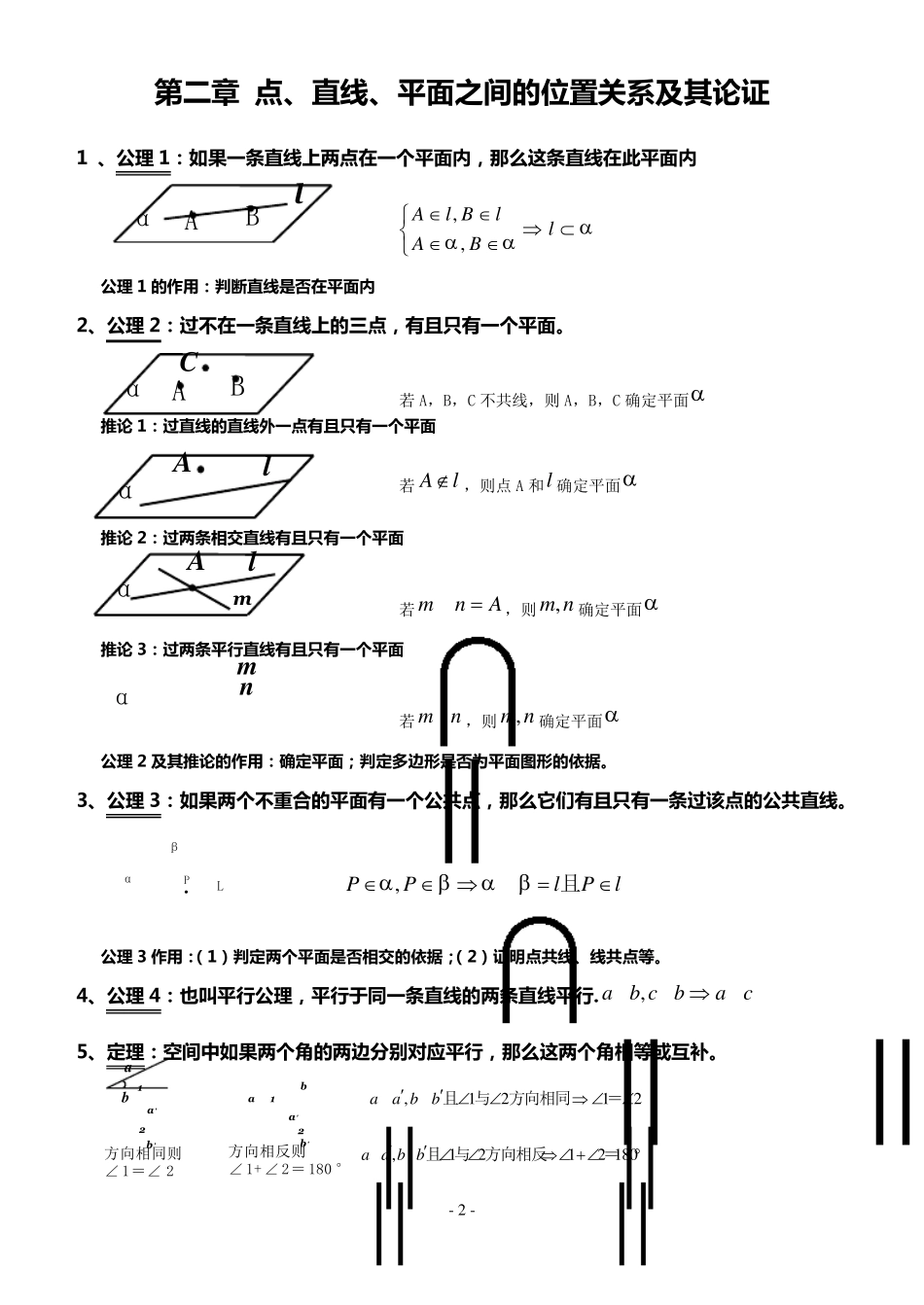
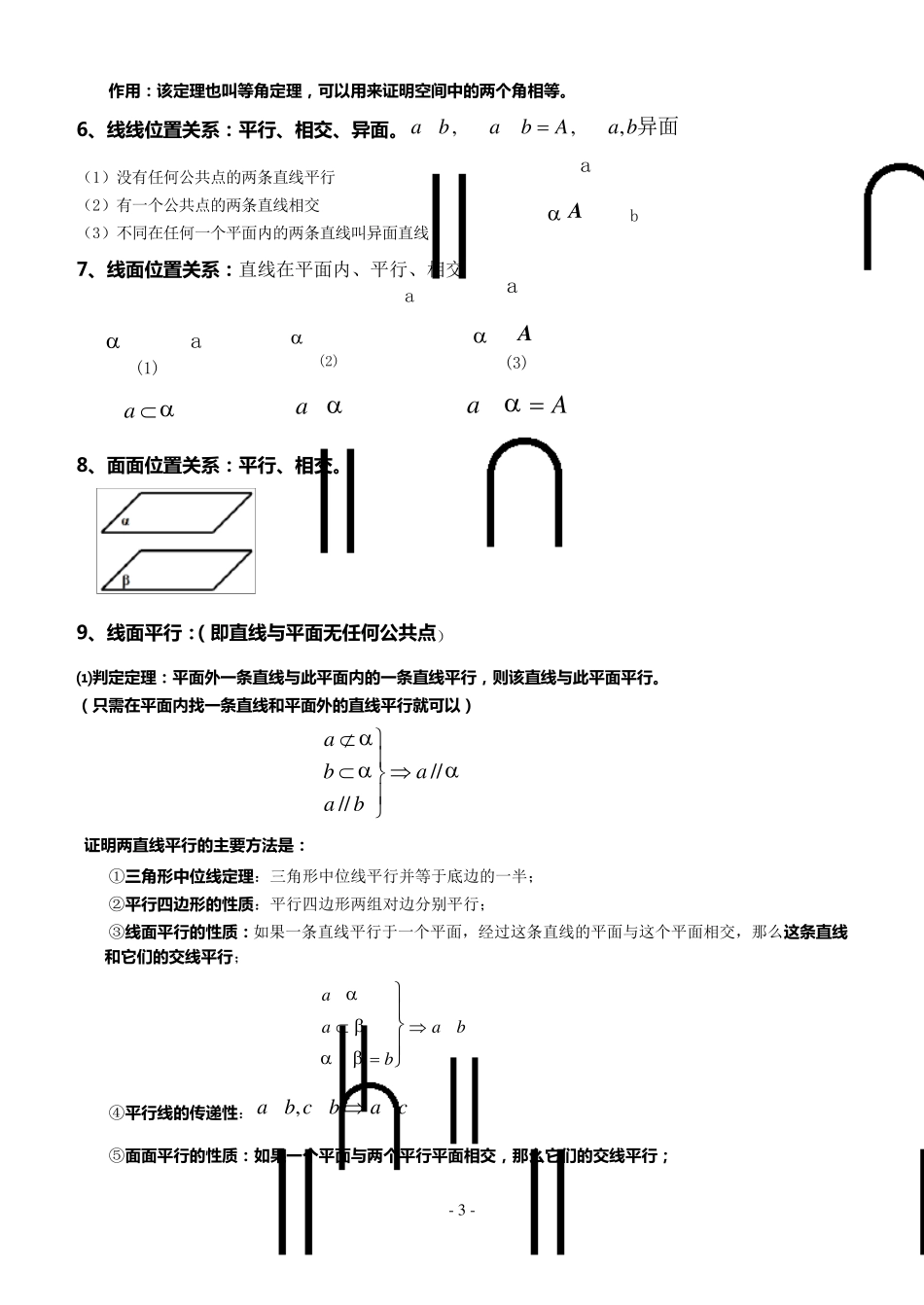
- 1 - 第 一 章 空 间 几 何 体 知 识 点 归 纳 1、 空 间 几 何 体 的 结 构 : 空 间 几 何 体 分 为 多 面 体 和 旋 转 体 和 简 单 组 合 体 ⑴常见的多 面 体 有:棱柱、棱锥、棱台;常见的旋 转 体 有:圆柱、圆锥、圆台、球。简单组合体的构成形式: 一种是由简单几何体拼接而成,一种是由简单几何体截去或挖去一部分而成。 ⑵ 棱 柱 :有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。 ⑶ 棱 台 : 用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。 1、 空 间 几 何 体 的 三 视 图 和 直 观 图 投影:中心投影 平行投影 (1 )定义:几何体的正 视 图 、 侧 视 图 和 俯 视 图统称为几何体的三 视 图 。 (2 )三视图中反应的长、宽、高的特点:“长对正 ”,“高平齐”,“宽相等” 2、 空 间 几 何 体 的 直 观 图 (表示空间图形的平面图). 观察者站在某一点观察几何体,画出的图形. 3、 斜二测画法的 基本步骤: ①建立适当直 角坐标系 xOy (尽可能使更多的点在坐标轴上) ②建立斜坐标系'''x O y,使'''x O y=450(或1350),注意它们确定的平面表示水平平面; ③画对应图形,在已知图形平行于X 轴的线段,在直观图中画成平行于X‘轴,且长度保持不变;在已知图形平行于Y 轴的线段,在直观图中画成平行于Y‘轴,且长度变为原来的一半; 一 般地,原图 的 面 积是其直 观 图 面 积的 22 倍,即22SS原图直观= 4、 空 间 几 何 体 的 表面 积与体 积 ⑴圆柱 侧 面 积;lrS 2侧面⑵ 圆锥侧 面 积:lrS 侧面 ⑶ 圆台 侧 面 积:()SrR l侧面 ⑷体 积公式: hSV柱体;hSV 31锥体; 13Vh SSSS下下台体上上 ⑸球的 表面 积和 体 积: 32344RVRS球球,.一 般地,面 积比等于相似比的 平方,体 积比等于相似比的 立方。 O 2O 1hlrR - 2 - 第 二 章 点 、直线、平面之间的位置关系及其论证 1 、公理 1:如果一条直线上两点 在一个平面内,那么这条直线在此平面内 ,,Al BllAB 公理 1 的作用:判断直线是否在平面内 2、公理 2:过不在一条直线...