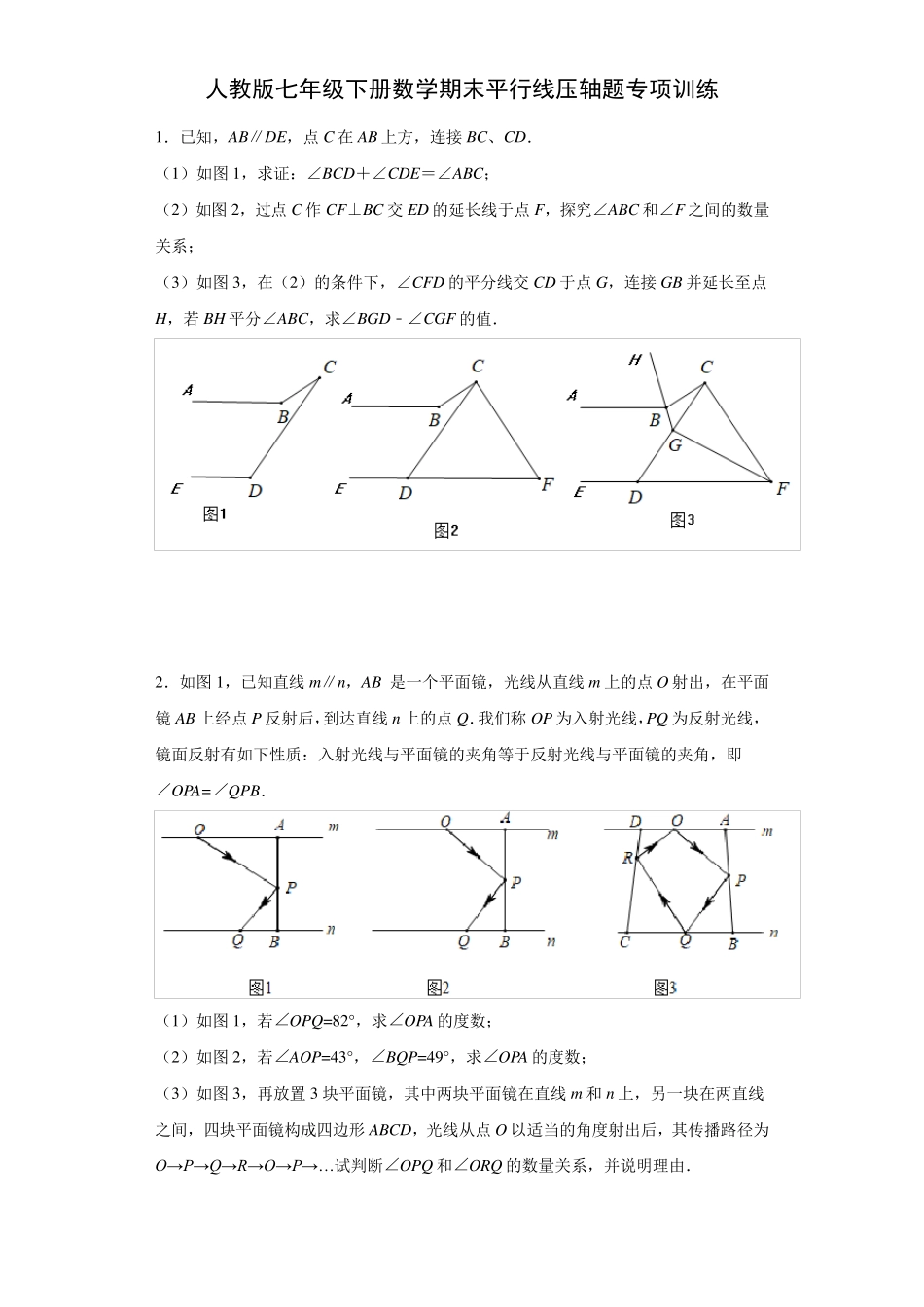
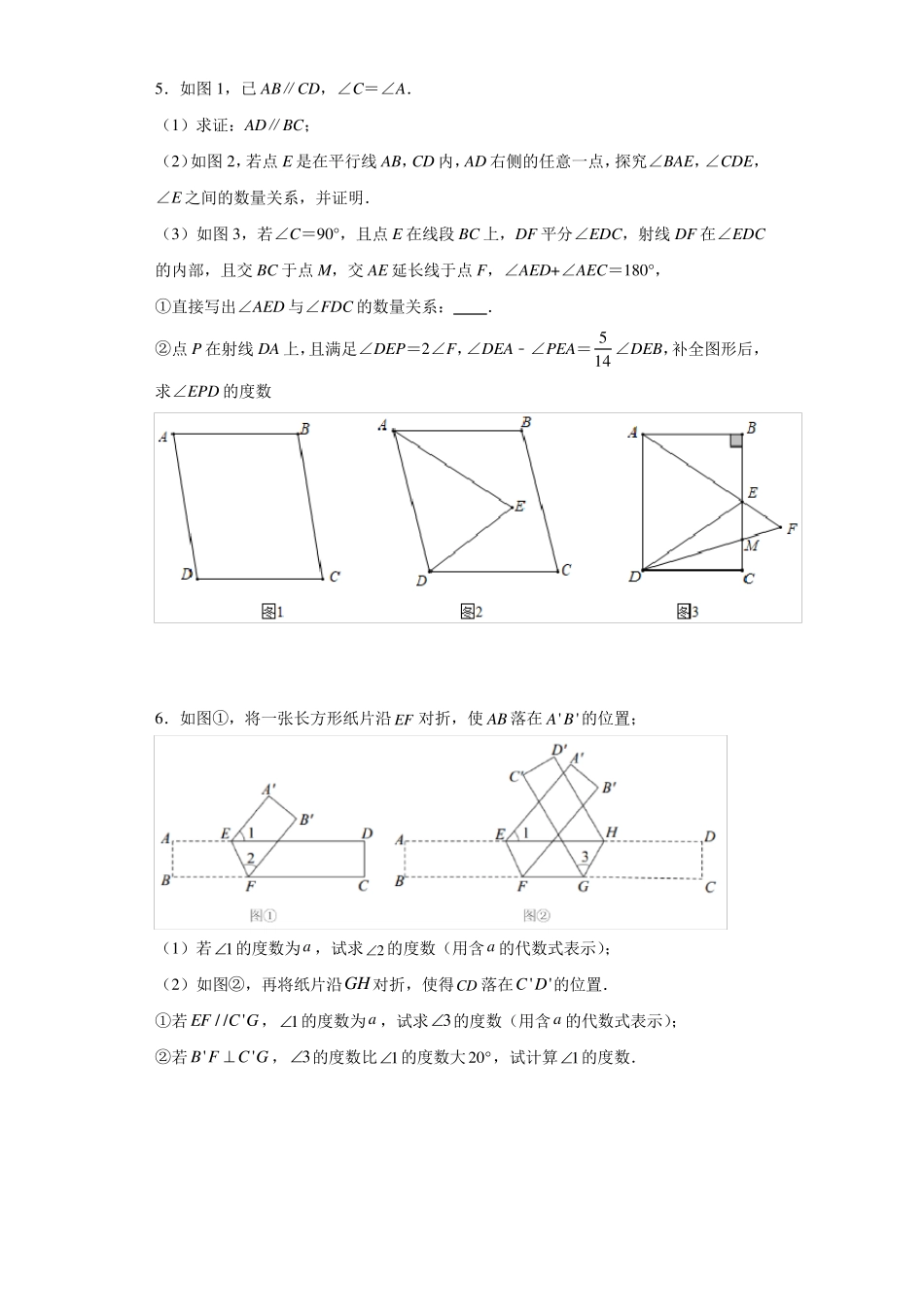
人教版七年级下册数学期末平行线压轴题专项训练 1.已知,AB∥DE,点C 在AB 上方,连接BC、CD. (1)如图1,求证:∠BCD+∠CDE=∠ABC; (2)如图2,过点C 作 CF⊥BC 交 ED 的延长线于点F,探究∠ABC 和∠F 之间的数量关系; (3)如图3,在(2)的条件下,∠CFD 的平分线交 CD 于点G,连接GB 并延长至点H,若 BH 平分∠ABC,求∠BGD﹣∠CGF 的值. 2.如图1,已知直线 m∥n,AB 是一个平面镜,光线从直线 m 上的点O 射出,在平面镜 AB 上经点P 反射后,到达直线 n上的点Q.我们称 OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OPA=∠QPB. (1)如图1,若∠OPQ=82°,求∠OPA 的度数; (2)如图2,若∠AOP=43°,∠BQP=49°,求∠OPA 的度数; (3)如图3,再放置 3 块平面镜,其中两块平面镜在直线 m 和 n上,另一块在两直线之间,四块平面镜构成四边形 ABCD,光线从点O 以适当的角度射出后,其传播路径为 O→ P→ Q→ R→ O→ P→ …试判断∠OPQ 和∠ORQ 的数量关系,并说明理由. 3.(1)(问题)如图1,若//AB CD , 40AEP ,130PFD .求EPF的度数; (2)(问题迁移)如图2,//AB CD ,点P在AB 的上方,问PEA,PFC,EPF之间有何数量关系?请说明理由; (3)(联想拓展)如图3 所示,在(2)的条件下,已知EPF,PEA的平分线和PFC的平分线交于点G ,用含有 的式子表示G的度数. 4.已知AB//CD. (1)如图1,E 为AB,CD 之间一点,连接BE,DE,得到∠BED.求证:∠BED=∠B+∠D; (2)如图,连接AD,BC,BF 平分∠ABC,DF 平分∠ADC,且 BF,DF 所在的直线交于点F. ①如图2,当点B 在点A 的左侧时,若∠ABC=50°,∠ADC=60°,求∠BFD 的度数. ②如图3,当点B 在点A 的右侧时,设∠ABC=α,∠ADC=β,请你求出∠BFD 的度数.(用含有α,β 的式子表示) 5.如图1,已AB∥CD,∠C=∠A. (1)求证:AD∥BC; (2)如图2,若点 E 是在平行线 AB,CD 内,AD 右侧的任意一点,探究∠BAE,∠CDE,∠E 之间的数量关系,并证明. (3)如图3,若∠C=90°,且点 E 在线段 BC 上,DF 平分∠EDC,射线 DF 在∠EDC的内部,且交 BC 于点 M,交 AE 延长线于点 F,∠AED+∠AEC=180°, ①直接写出∠AED 与∠FDC 的数量...