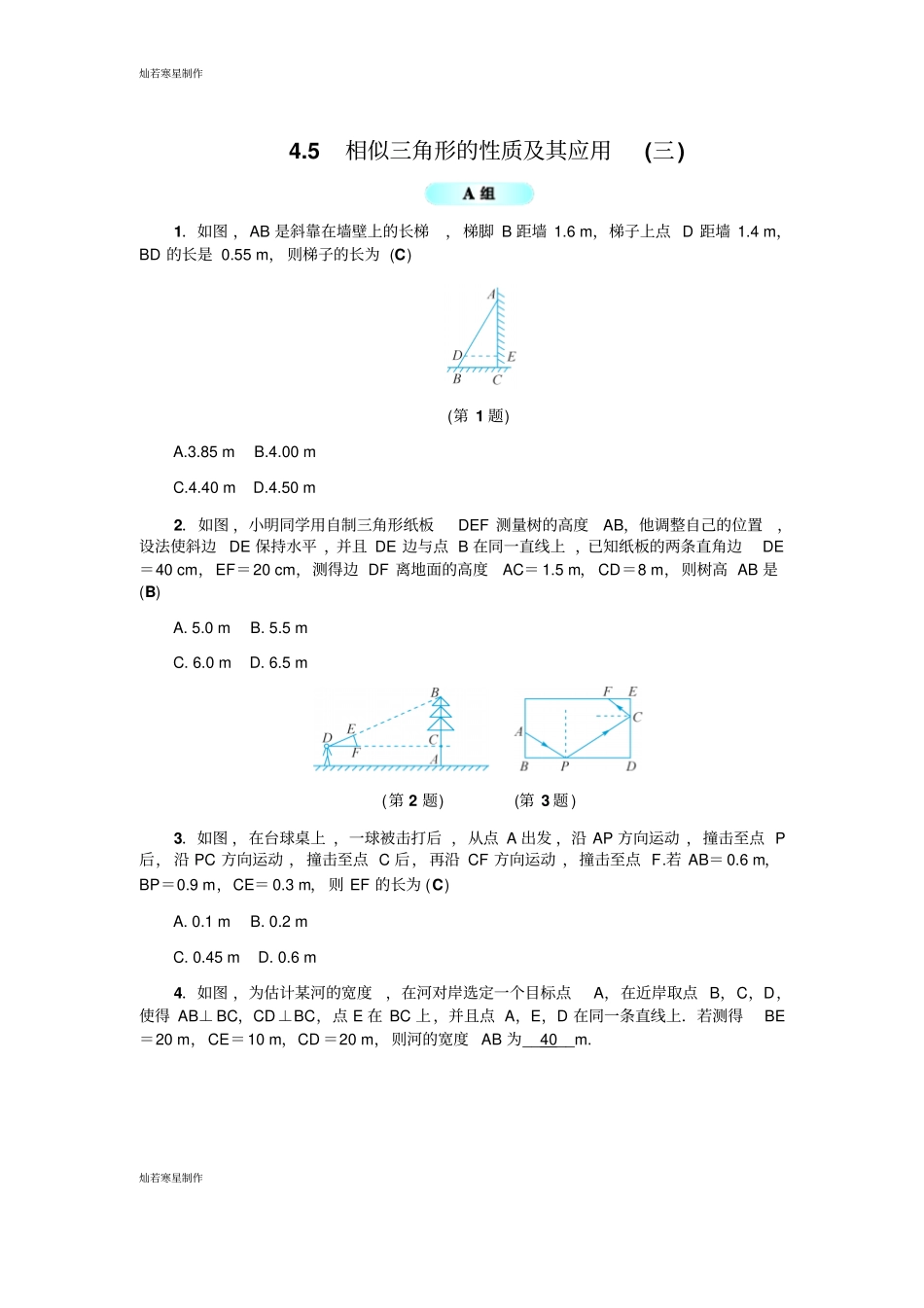
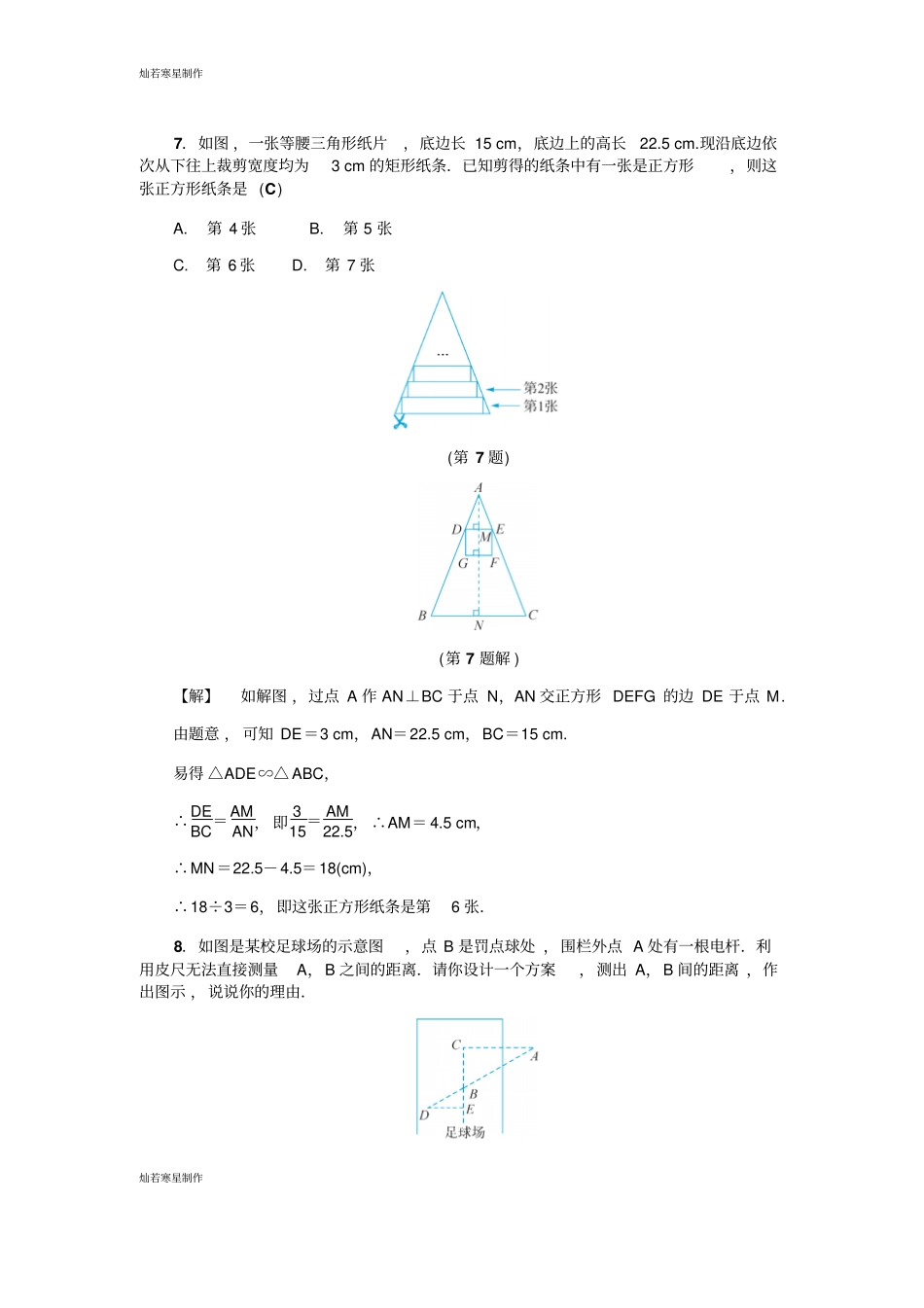
灿若寒星制作灿若寒星制作4.5 相似三角形的性质及其应用(三)1.如图 ,AB 是斜靠在墙壁上的长梯,梯脚 B 距墙 1.6 m,梯子上点 D 距墙 1.4 m,BD 的长是 0.55 m, 则梯子的长为 (C) (第 1 题) A.3.85 m B.4.00 m C.4.40 m D.4.50 m 2.如图 ,小明同学用自制三角形纸板DEF 测量树的高度AB,他调整自己的位置,设法使斜边DE 保持水平 ,并且 DE 边与点 B 在同一直线上 ,已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边 DF 离地面的高度AC= 1.5 m, CD=8 m,则树高 AB 是(B) A. 5.0 m B. 5.5 m C. 6.0 m D. 6.5 m (第 2 题)(第 3 题 ) 3.如图 ,在台球桌上 ,一球被击打后 ,从点 A 出发 ,沿 AP 方向运动 ,撞击至点 P后, 沿 PC 方向运动 ,撞击至点 C 后,再沿 CF 方向运动 ,撞击至点 F.若 AB= 0.6 m,BP=0.9 m,CE= 0.3 m, 则 EF 的长为 (C) A. 0.1 m B. 0.2 m C. 0.45 m D. 0.6 m 4.如图 ,为估计某河的宽度,在河对岸选定一个目标点A,在近岸取点 B,C,D,使得 AB⊥ BC,CD⊥BC,点 E 在 BC 上,并且点 A,E,D 在同一条直线上.若测得BE=20 m,CE=10 m,CD =20 m,则河的宽度AB 为__40__m. 灿若寒星制作灿若寒星制作(第 4 题)(第 5 题) 5.如图 ,为了测量旗杆AB 的高度 ,某同学画出了示意图,BA⊥EA 于点 A,DC⊥EA 于点 C,并把测量结果记录如下:CD=a,CA=b,CE=c.请你帮助该同学计算旗杆 AB 的高度 (用含 a,b,c 的代数式表示 ).【解】 DC⊥ AE,BA⊥AE, ∴DC∥ BA,∴△ ECD∽△EAB,∴CDAB =CEAE, 即 aAB=cc+b,∴AB= a(c+b)c=a+abc . (第 6 题) 6.如图 ,水平放置的一圆柱形油桶高1.5 m,用一根 2 m 长的木棒从桶盖小口A 处斜插至油桶底部对角B 处,抽出木棒后 ,量得上面没浸油的部分为1.2 m,求桶内油面的高度 (木棒的粗细忽略不计).【解】根据题意 ,得 DE∥BC,∴△ ADE∽△ABC,∴AEAC=ADAB,即AE1.5=1.22 ,解得 AE=0.9(m).∴EC= AC-AE=0.6 m,即桶内油面的高度为0.6 m. 灿若寒星制作灿若寒星制作7.如图 ,一张等腰三角形纸片,底边长 15 cm,底边上的高长22.5 cm.现沿底边依次从下往上裁剪宽度均为3 cm 的矩形纸条.已知剪得的纸条中有一张是正方形,则这张正方形纸条是 (C) A. 第...