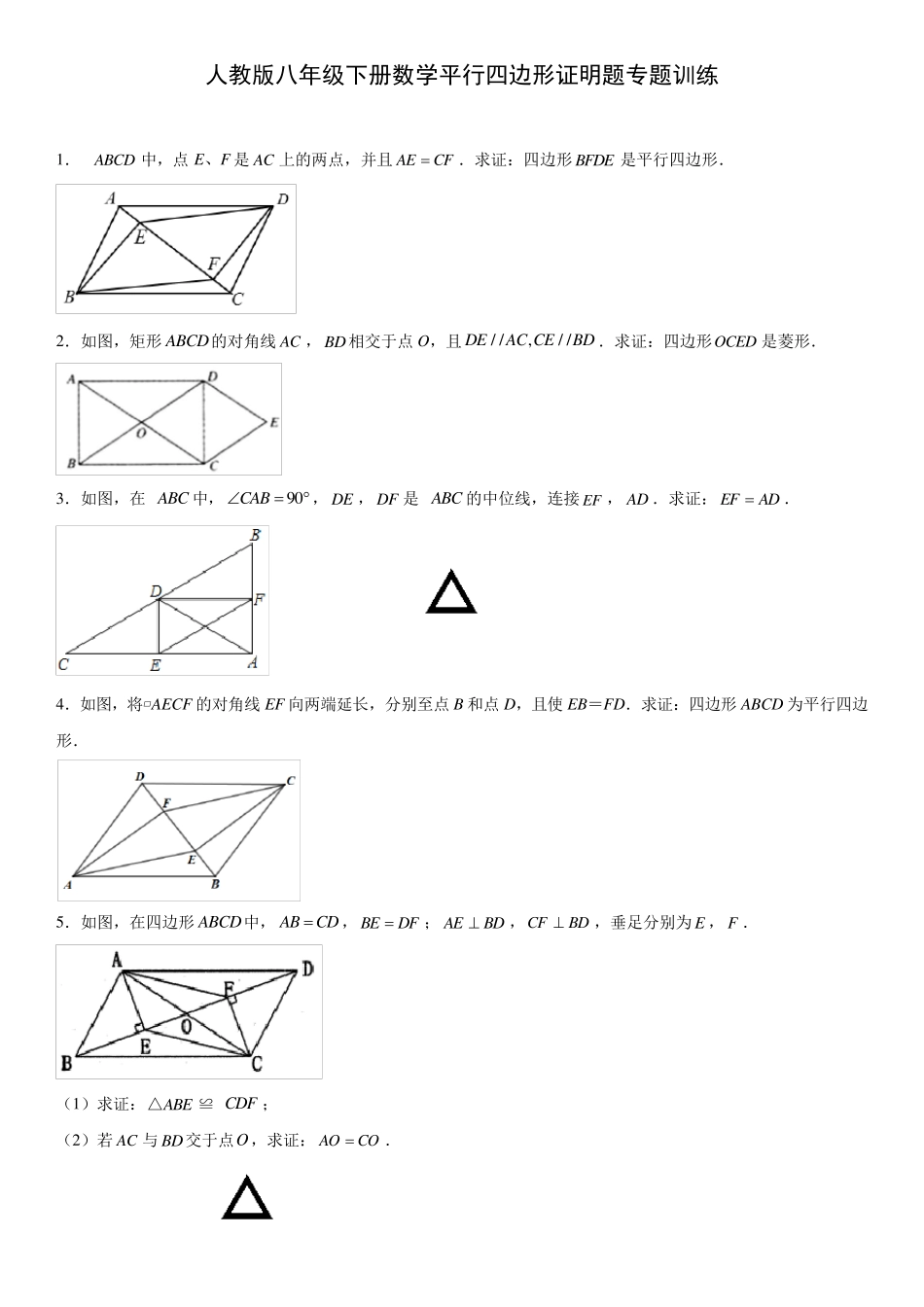
人教版八年级下册数学平行四边形证明题专题训练 1 .ABCD 中,点E、F 是AC 上的两点,并且AECF.求证:四边形BFDE 是平行四边形. 2 .如图,矩形ABCD的对角线AC ,BD相交于点O,且/ /,/ /DEAC CEBD .求证:四边形OCED 是菱形. 3 .如图,在ABC 中,9 0CAB,DE ,DF 是ABC 的中位线,连接EF ,AD .求证:EFAD. 4 .如图,将▱ AECF 的对角线EF 向两端延长,分别至点B 和点D,且使EB=FD.求证:四边形ABCD 为平行四边形. 5 .如图,在四边形ABCD中,ABCD,BEDF;AEBD,CFBD,垂足分别为E ,F . (1 )求证:ABE△≌ CDF ; (2 )若 AC 与 BD交于点O ,求证:AOCO. 6.如图,在ABCD 中,点E ,F 分别在AD 、BC 上,且AECF,连接EF ,AC 交于点O .求证:OEOF. 7.已知:如图,矩形ABCD 中,O 是AC 与BD 的交点,过O 点的直线EF 与AB、CD 的延长线分别相交于点E、F. (1)求证:△BOE≌△DOF; (2)当EF 与AC 满足什么关系时,以A、E、C、F 为顶点的四边形是菱形?并给出证明. 8.如图,在△ABC 中,D 是BC 边上的一点,E 是AD 的中点,过A 点作BC 的平行线交CE 的延长线于F,且AF=BD,连接BF. (1)求证:D 是BC 的中点 (2)如果AB=AC,试判断四边形AFBD 的形状,并证明你的结论. 9.如图,菱形ABCD 的对角线AC、BD 相交于点O,过点D 作DE∥AC 且DE=12 AC,连接CE、OE,连接AE 交OD 于点F. (1)求证:OE=CD; (2)若菱形ABCD 的边长为2,∠ABC=60°,求AE 的长. 10.如图,在矩形ABCD 中,AB=6,BC=10,点E 在边CD 上,连接AE,将四边形ABCE 沿直线AE 折叠,得到多边形AB C E ,且B C 恰好经过点D. (1)线段DC′的长度; (2)求ADE 的面积. 11.如图,在四边形ABCD 中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E、F. (1)求证:△ABE≌△CDF; (2)若AC 与BD 交于点O,求证:AO=CO. 12.如图将矩形ABCD 沿对角线AC 对折,使△ABC 落在△ACE 的位置,且CE 与AD 相交于点F,求证:EF=DF. 13.如图,在四边形ABCD 中,AB=AD,CB=CD,E 是CD 上一点,BE 交AC 于点F,连接DF. (1)求证:∠BAC=∠DAC,∠AFD=∠CFE; (2)若AB∥CD,试证明四边形ABCD 是菱形; (3)在(2)的条件下,试确定 E 点的位置,使∠EFD=∠BCD,并说明理由. 14.如...