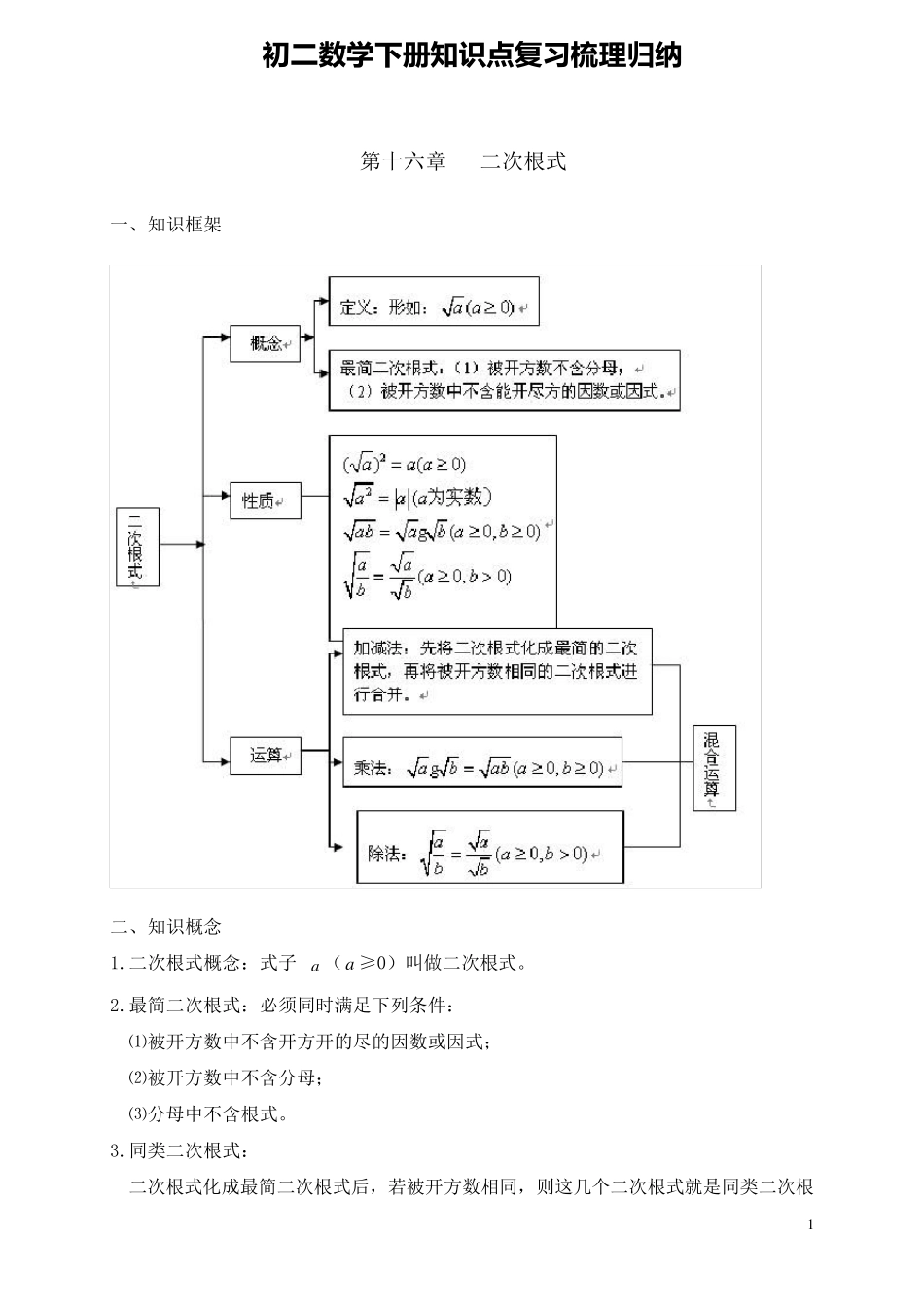
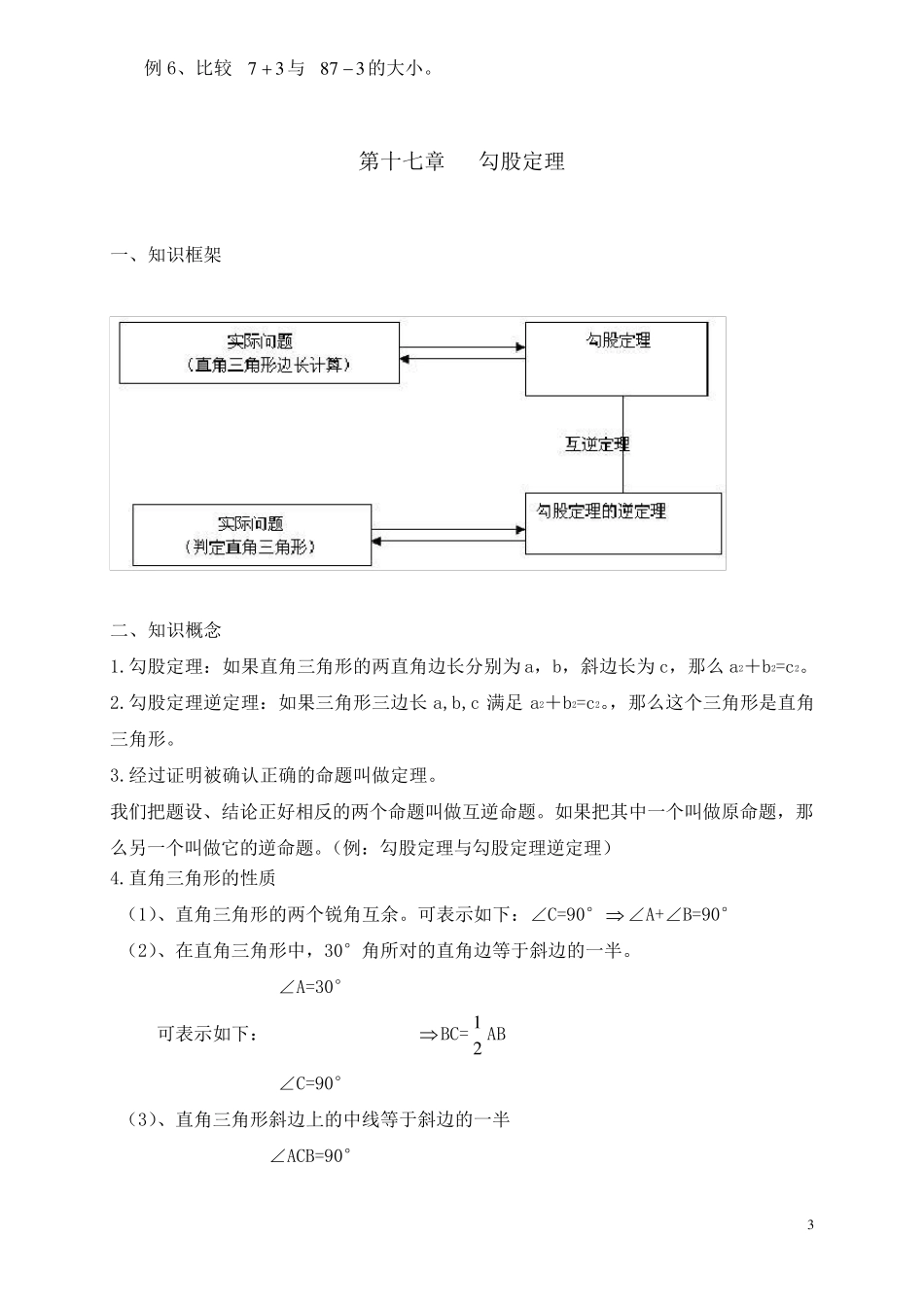
1 初 二 数 学 下册知识点复习梳理归纳 第十六章 二次根式 一、知识框架 二、知识概念 1.二次根式概念:式子a (a ≥0)叫做二次根式。 2.最简二次根式:必须同时满足下列条件: ⑴被开方数中不含开方开的尽的因数或因式; ⑵被开方数中不含分母; ⑶分母中不含根式。 3.同类二次根式: 二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根 2 式。 4.二次根式的性质: (1)(a )2= a (a ≥0); (2) aa 2 5.二次根式的运算: (1)因式的外移和内移:如果被开方数中有的因式能够开得尽方,那么,就可以用它的算术根代替而移到根号外面;如果被开方数是代数和的形式,那么先解因式,•变形为积的形式,再移因式到根号外面,反之也可以将根号外面的正因式平方后移到根号里面. (2)二次根式的加减法:先把二次根式化成最简二次根式再合并同类二次根式. (3)二次根式的乘除法:二次根式相乘(除),将被开方数相乘(除),所得的积(商)仍作积(商)的被开方数并将运算结果化为最简二次根式. ab =a ·b (a≥0,b≥0); bbaa(b≥0,a>0). (4)有理数的加法交换律、结合律,乘法交换律及结合律,•乘法对加法的分配律以及多项式的乘法公式,都适用于二次根式的运算. △ 比 较 数 值的方法 (1)、根式变形法 当0 ,0ab时,①如果ab,则ab;②如果ab,则ab。 (2)、平方法 当0 ,0ab时,①如果22ab,则 ab;②如果22ab,则ab。 (3)、分母有理化法 通过分母有理化,利用分子的大小来比较。 例 3、比较231与121的大小。 (4)、分子有理化法 通过分子有理化,利用分母的大小来比较。 例 4、比较 1 51 4与 1 41 3的大小。 (5)、倒数法 例 5、比较76与65的大小。 a (a >0) a(a <0) 0 (a =0); 3 例6、比较73与8 73 的大小。 第十七章 勾股定理 一、知识框架 二、知识概念 1.勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2。 2.勾股定理逆定理:如果三角形三边长a,b,c 满足a2+b2=c2。,那么这个三角形是直角三角形。 3.经过证明被确认正确的命题叫做定理。 我们把题设、结论正好相反的两个命题叫做互逆命题。如果把其中一个叫做原命题,那么另一个叫做它的逆命题。(例:勾股定理与勾股定理逆定理) 4.直角三角形的性质 ...