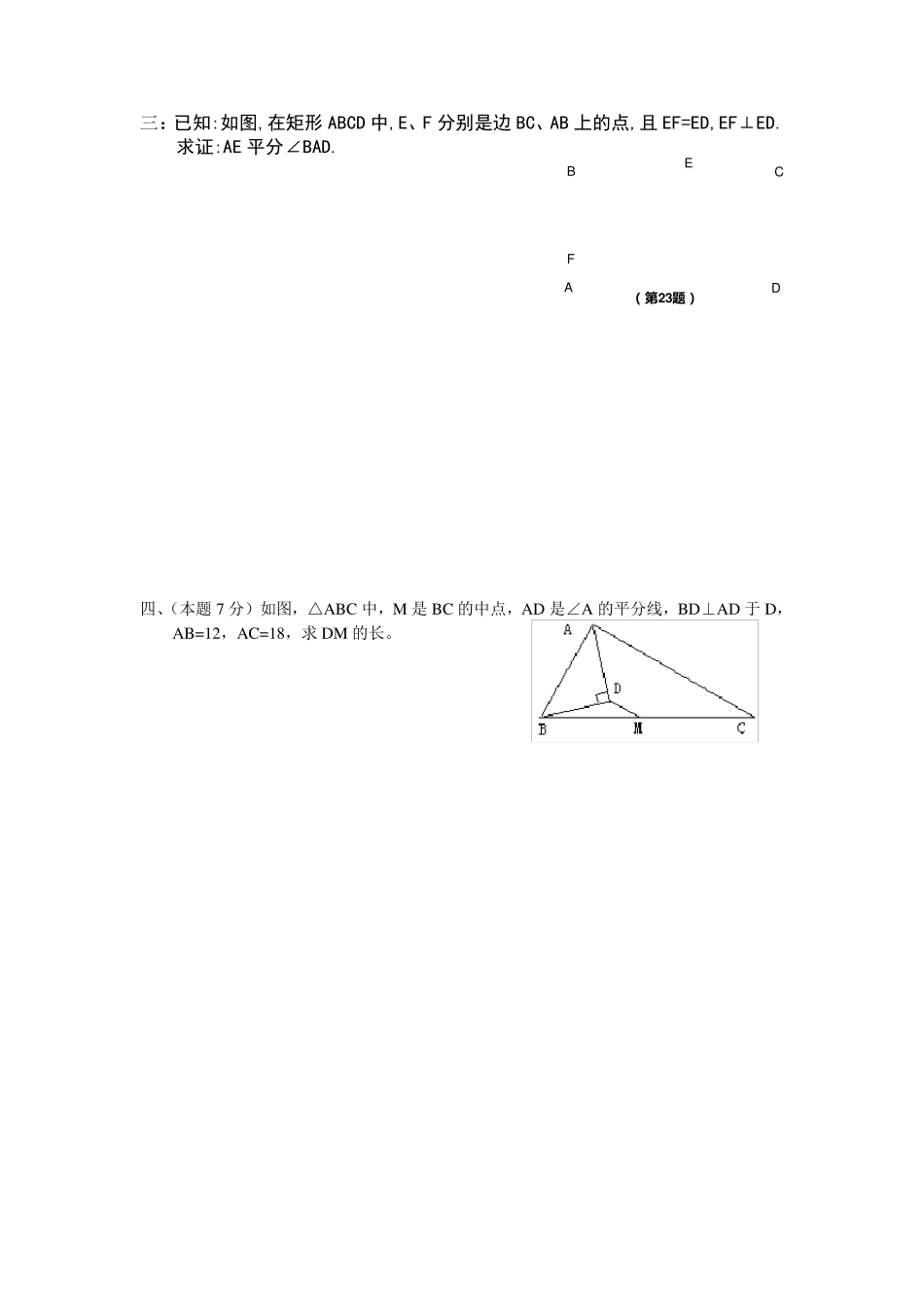
一:已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC 于点 F,交 BC 于点 G,交 AB 的延长线于点 E,且 AEAC. (1)求证:BGFG; (2)若2ADDC,求 AB 的长. 二:如图,已知矩形ABCD,延长 CB 到 E,使 CE=CA,连结 AE 并取中点 F,连结AE 并取中点 F,连结 BF、DF,求证 BF⊥DF。 D C E B G A F 三:已知:如图,在矩形ABCD 中,E、F 分别是边BC、AB 上的点,且EF=ED,EF⊥ED.求证:AE 平分∠BAD. 四、(本题7 分)如图,△ABC 中,M 是BC 的中点,AD 是∠A 的平分线,BD⊥AD 于 D,AB=12,AC=18,求 DM 的长。 ( 第23题)ECDBAF五、(本题8 分)如图,四边形ABCD 为等腰梯形,AD∥BC,AB=CD,对角线 AC、BD交于点 O,且 AC⊥BD,DH⊥BC。 ⑴求证:DH= 21(AD+BC) ⑵若 AC=6,求梯形ABCD 的面积。 六、(6 分) 、如图,P 是正方形ABCD 对角线 BD 上一点,PE⊥DC,PF⊥BC,E、F 分别为垂足,若 CF=3,CE=4,求 AP 的长. 七、(8 分)如图,等腰梯形ABCD中,AD∥BC,M、N 分别是AD、BC 的中点,E、F 分别是BM、CM 的中点. (1)在不添加线段的前提下,图中有哪几对全等三角形?请直接写出结论; (2)判断并证明四边形MENF是何种特殊的四边形? (3)当等腰梯形ABCD的高h 与底边BC 满足怎样的数量关系时?四边形MENF是正方形(直接写出结论,不需要证明). 选择题: 15、如图,每一个图形都是由不同个数的全等的小等腰梯形拼成的,梯形上、下底及腰长如图,依此规律第10 个图形的周长为 。 …… 第一个图 第二个图 第三个图 16、如图,矩形ABCD 对角线AC 经过原点O,B 点坐标为 (―1,―3),若一反比例函数xky的图象过点D,则其 解析式为 。 MFENDCAB一:解:(1)证明:90ABCDEAC°,⊥于点 F , ABCAFE . ACAEEAFCAB ,, ABCAFE△≌△ ABAF. 连接 AG , AG=AG,AB=AF, RtRtABGAFG△≌△. BGFG. (2)解: AD=DC,DF⊥AC, 1122AFACAE. 30E °. 30FADE °, 3AF. 3ABAF. 二:证明: CE=CA AF=EF ∴CF⊥AE ∠AFC=∠EFC=90 在直角三角形 AEB 中,BF 是斜边上中线 ∴BF=AF 又: AD=BC CF=CF ∴△BCF≌△ADF ∠BFC=∠AFD 而∠AFD+∠DFC=AFC=90 ∴∠BFC+∠DFC=∠BFD=90 BF⊥DF 三:证明: 四边...