力学郑永令练习题解答

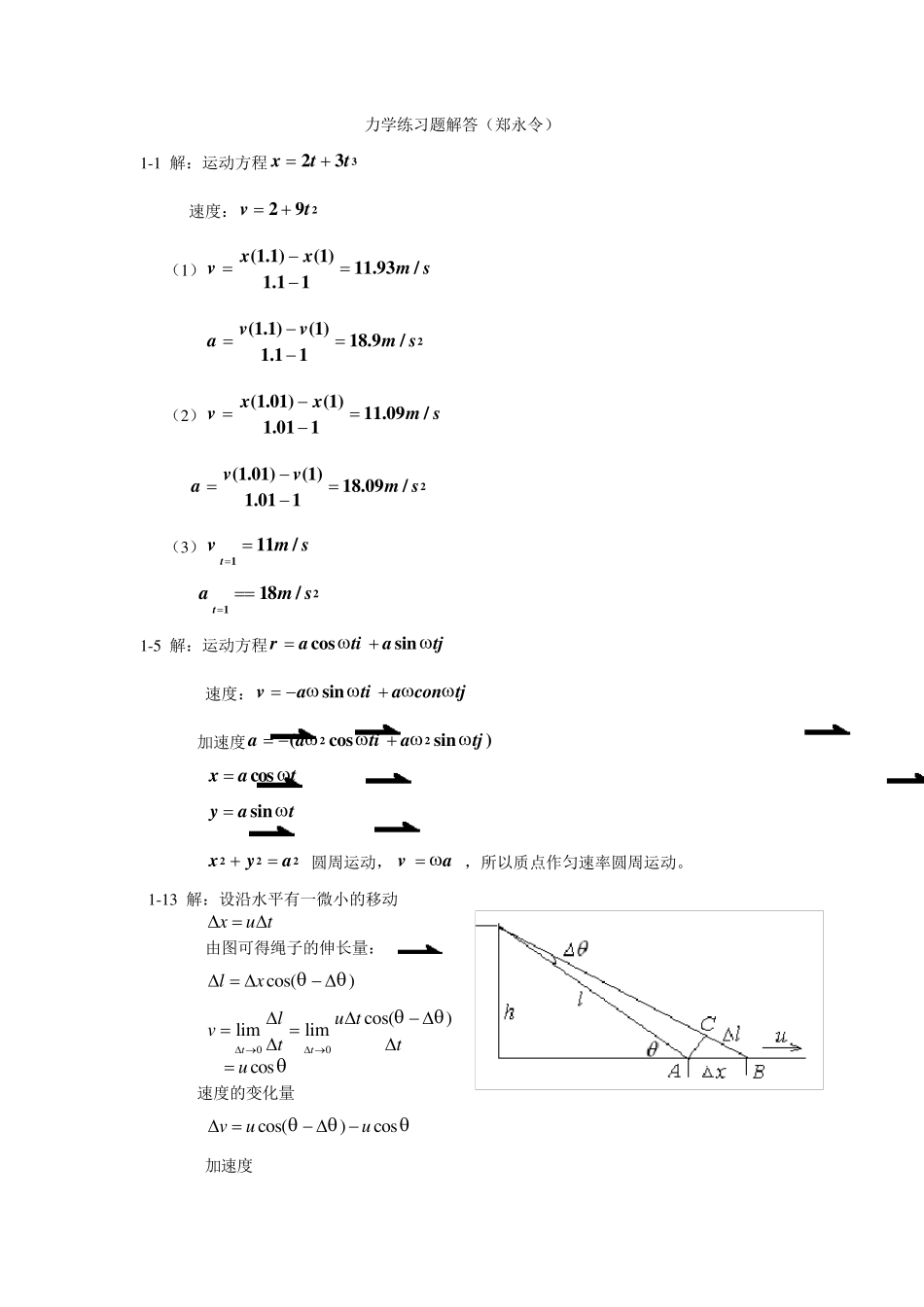
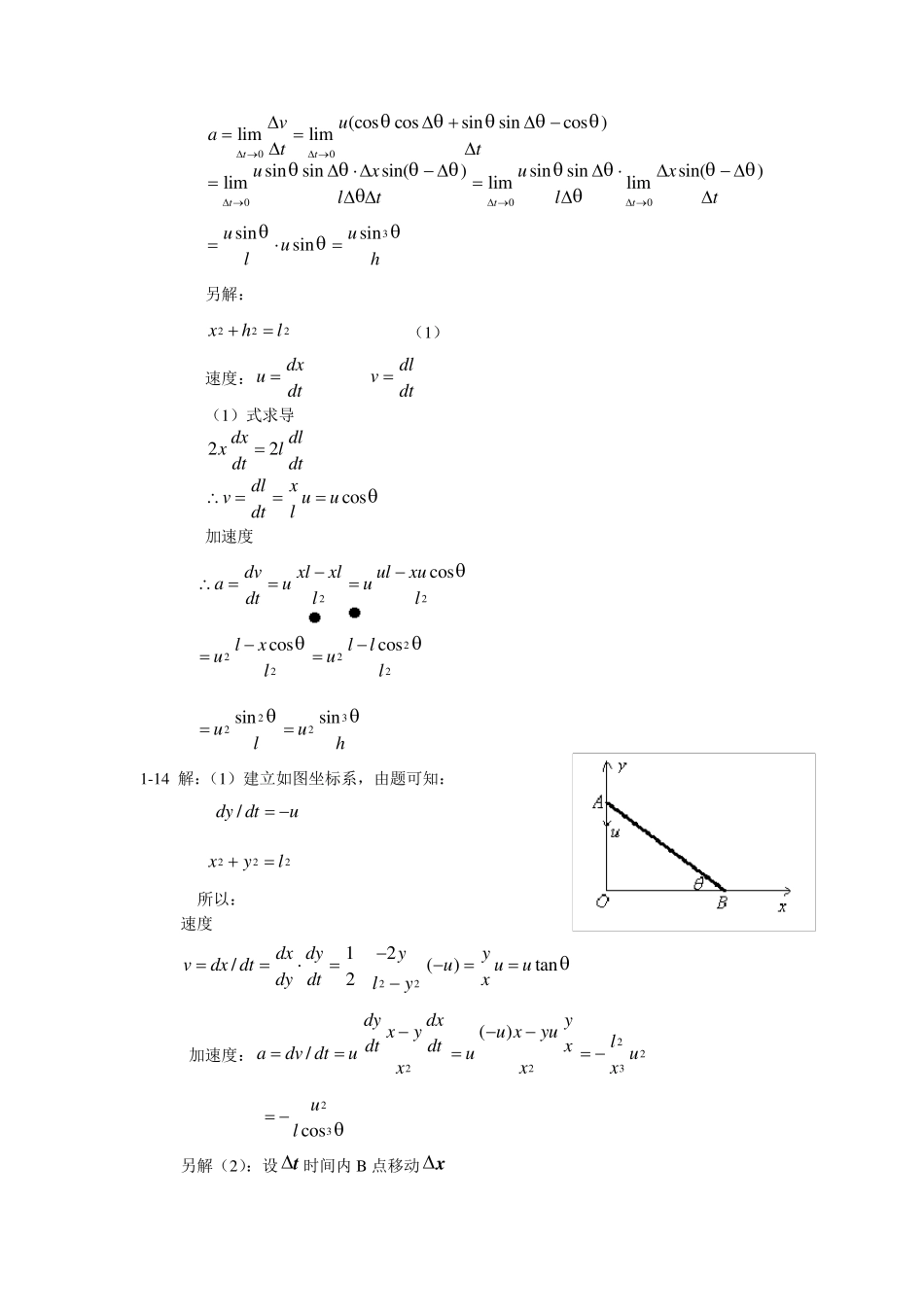
力学练习题解答（郑永令） 1-1 解：运动方程323xtt 速度：229vt （1）(1.1)(1)11.93/1.11xxvm s 2(1.1)(1)18.9/1.11vvam s （2）(1.01)(1)11.09/1.011xxvm s 2(1.01)(1)18.09/1.011vvam s （3）111/tvm s  2118/tam s  1-5 解：运动方程cossinratiatj 速度：sinvatia con tj  加速度22(cossin)aatiatj  cosxat sinyat 222xya 圆周运动，va ，所以质点作匀速率圆周运动。 1-13 解：设沿水平有一微小的移动 xu t   由图可得绳子的伸长量： cos()lx    00cos()limlimttlu tvtt    cosu 速度的变化量 cos()cosvuu   加速度 00(coscossinsincos )limlimttvuatt   000sinsinsin()sinsinsin()limlimlimtttuxuxltlt         3sinsinsinuuulh 另解： 222xhl （1） 速度：dxdluvdtdt （1）式求导 22dxdlxldtdt cosdlxvuudtl 加速度 22cosdvxlxlulxuauudtll 22222coscoslxlluull 2322sinsinuulh 1-14 解：（1）建立如图坐标系，由题可知： /dy dtu  222xyl 所以： 速度 2212/()tan2dx dyyyvdx dtuuudy dtxly 加速度：22223()/dydxyxyu xyuldtdtxadv dtuuuxxx  23cosul  另解（2）：设 t 时间内 B 点移动x 则：22()()xxyu tl   速度 222200()limlimttlyu tlyxvtt  22222222220(() )()lim(())tlyu tlylyu tlyt   2222202()lim(())tyu tu ty uxlyu tlyt   加速度 00()( )limlim[() /]ttv ttv tyu tyauuttxxx    223230lim ()txu ty xxyluuvuxx x txxx      23cosul  1-19 解：建立如图所示坐标 00 cosxvv 00 sinyvv sinxag  cosyag  所以，t时刻201cossin2xvtgt （1） 201sincos2yvtgt...