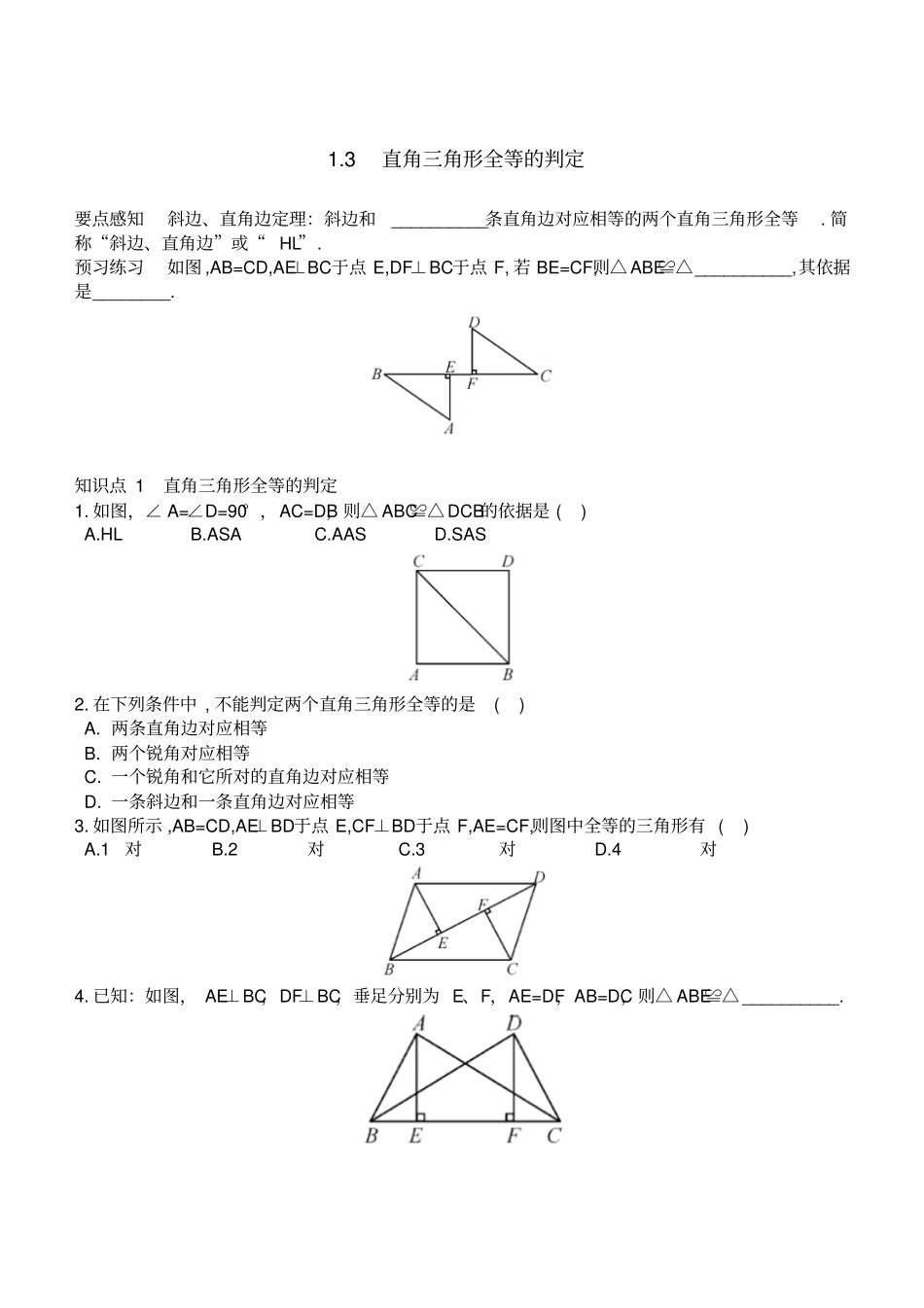
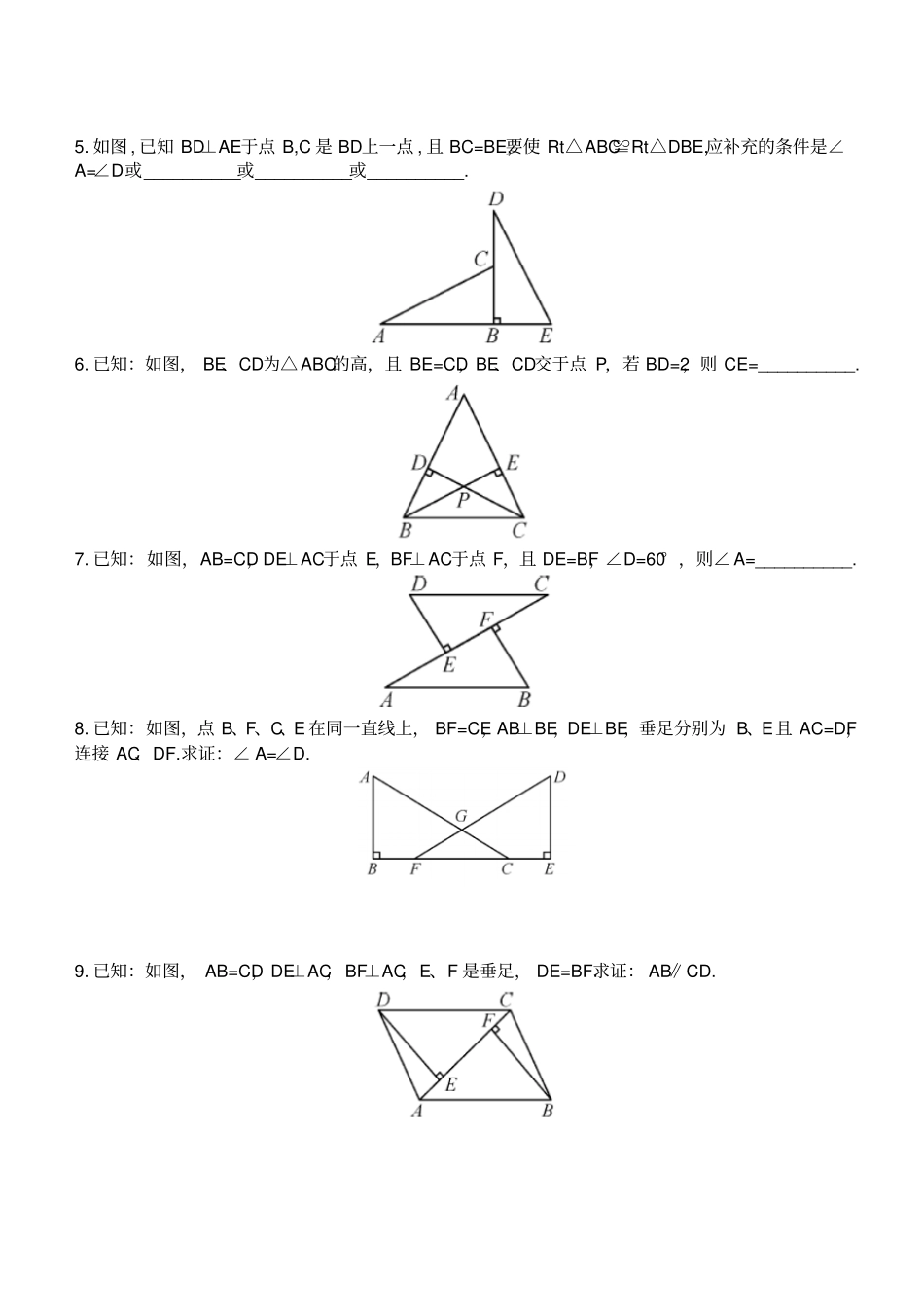
1.3 直角三角形全等的判定要点感知斜边、直角边定理:斜边和__________条直角边对应相等的两个直角三角形全等. 简称“斜边、直角边”或“ HL”. 预习练习如图 ,AB=CD,AE⊥BC于点 E,DF⊥BC于点 F, 若 BE=CF,则△ ABE≌△__________,其依据是________. 知识点 1 直角三角形全等的判定1. 如图,∠ A=∠D=90° ,AC=DB,则△ ABC≌△ DCB的依据是 ( ) A.HL B.ASA C.AAS D.SAS 2. 在下列条件中 , 不能判定两个直角三角形全等的是( ) A. 两条直角边对应相等 B. 两个锐角对应相等 C. 一个锐角和它所对的直角边对应相等 D. 一条斜边和一条直角边对应相等3. 如图所示 ,AB=CD,AE⊥BD于点 E,CF⊥BD于点 F,AE=CF,则图中全等的三角形有 ( ) A.1对 B.2对 C.3对 D.4对4. 已知:如图, AE⊥BC,DF⊥BC,垂足分别为 E、F,AE=DF,AB=DC,则△ ABE≌△ __________. 5. 如图 , 已知 BD⊥AE于点 B,C 是 BD上一点 , 且 BC=BE,要使 Rt△ABC≌Rt△DBE,应补充的条件是∠A=∠D或__________或__________或__________. 6. 已知:如图, BE、CD为△ ABC的高,且 BE=CD,BE、CD交于点 P,若 BD=2,则 CE=__________. 7. 已知:如图,AB=CD,DE⊥AC于点 E,BF⊥AC于点 F,且 DE=BF,∠D=60° ,则∠ A=__________. 8. 已知:如图,点 B、F、C、E 在同一直线上, BF=CE,AB⊥BE,DE⊥BE,垂足分别为 B、E且 AC=DF,连接 AC、DF.求证:∠ A=∠D. 9. 已知:如图, AB=CD,DE⊥AC,BF⊥AC,E、F 是垂足, DE=BF.求证: AB∥CD. 知识点 2 作直角三角形10. 已知一条斜边和一条直角边,求作直角三角形,作图的依据是__________. 11. 已知 Rt△ABC,∠ ACB=90° ,请利用直角三角形全等的判定HL,求作三角形 Rt△DEF,使 Rt△DEF≌Rt△ABC. 12. 用三角尺可按下面方法画角平分线:如图,在已知∠ AOB两边上分别取 OM=ON,再分别过点 M、N作 OA、OB的垂线,两垂线交于点 P,画射线 OP,则 OP平分∠ AOB.作图过程用到了△ OPM≌△ OPN,那么△ OPM≌△OPN的依据是 __________. 13. 如图,△ ABC中,AD⊥BC于点 D,要使△ ABD≌△ACD,若根据“ HL”判定,还需要加一个条件__________. 14. 如图, 在 Rt△ABC的斜边 BC上截取 CD=CA,过点 D作 DE⊥BC交 AB于点 E,则有 ( ) A.DE=DB B.DE=AE C.AE=BE D.AE=BD 15. 如图, AD∥BC,∠A=90° ,E...