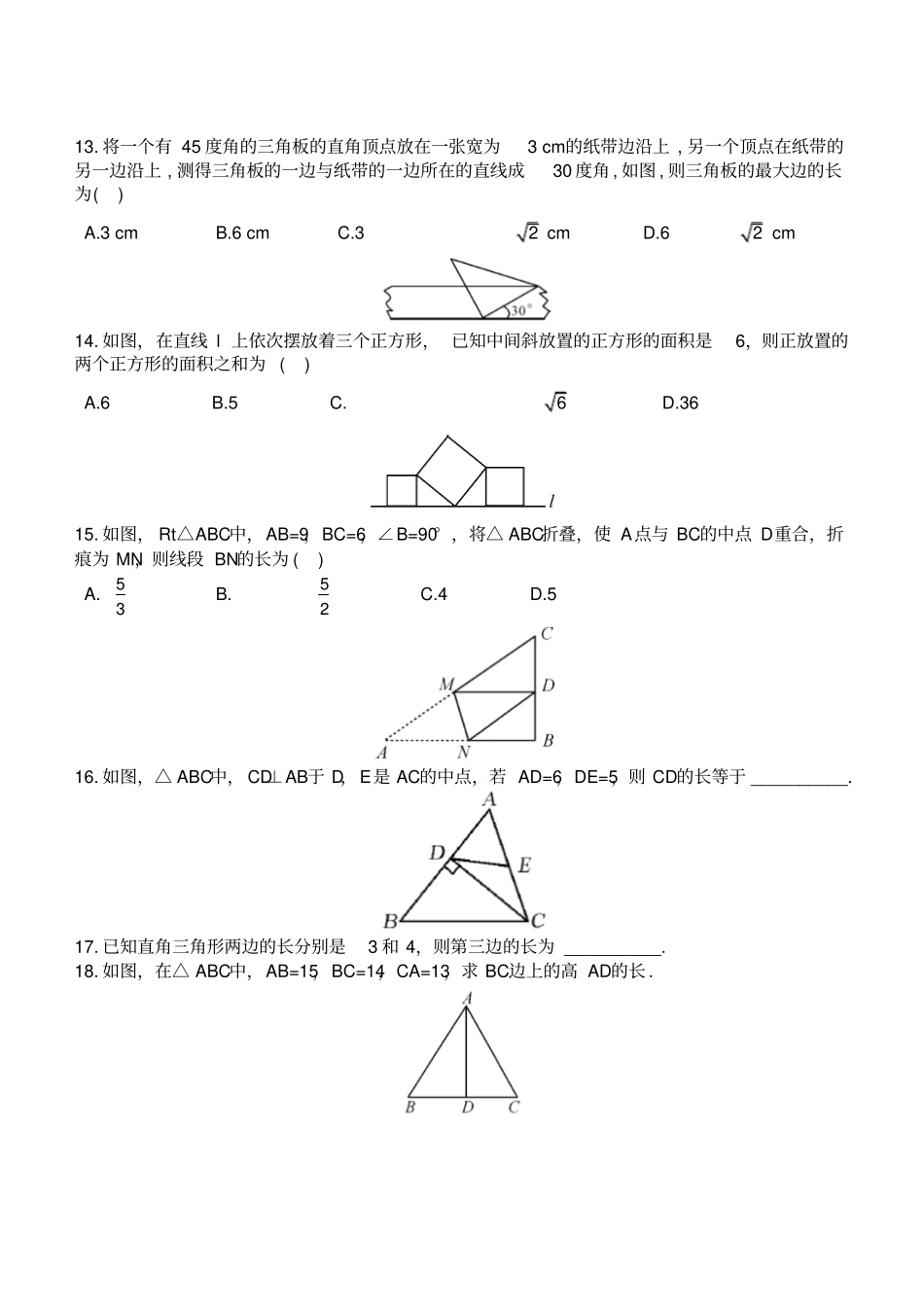
1.2 直角三角形的性质和判定( Ⅱ) 第 1 课时勾股定理要点感知直角三角形的性质定理 ( 勾股定理 ) :直角三角形两直角边a、b 的平方和等于__________的平方 . 即 a2+b2=c2. 预习练习△ABC中, ∠C=90° ,a 、b、c 分别是∠ A、∠ B、∠C的对边 . (1)若 a=5,b =12, 则 c=__________; (2)若 c=41,a =40, 则 b=__________. 知识点勾股定理1. 在△ ABC中,∠ C=90° ,如果 AB=10,BC∶AC=3∶4,那么 BC=( ) A.6 B.8 C.10 D.以上都不对2. 一个直角三角形的三边长为三个连续偶数,则它的斜边长为( ) A.6 B.8 C.10 D.12 3. 已知一个三角形三个内角的比是1∶2∶1, 则它的三条边的比是 ( ) A.1 ∶2 ∶1 B.1∶2∶1 C.1∶2 ∶3 D.1∶4∶1 4. 如图 , 长方形 OABC的边 OA长为 2, 边 AB长为 1,OA在数轴上 , 以原点 O为圆心 , 对角线 OB的长为半径画弧 , 交正半轴于一点 , 则这个点表示的实数是 ( ) A.2.5 B.22 C.3 D.55. 如图,点 D在△ ABC的边 AC上,将△ ABC沿 BD翻折后,点 A恰好与点 C重合 . 若 BC=5,CD=3,则 BD的长为 ( ) A.1 B.2 C.3 D.4 6. 在△ ABC中,∠ C=90° ,AB=7,BC=5,则边 AC的长为 __________. 7. 等腰△ ABC中, AB=AC=10 cm,BC=12 cm,则 BC边上的高是 __________cm. 8. 一个直角三角形的斜边长比直角长边大2,另一直角边长为6,则斜边长为 __________. 9. 如图,△ ABC中,AB=AC=20,BC=32,D是 BC上一点, AD=15,且 AD⊥AC,求 BD长. 10. 如图,在△ ABC中,∠ ACB=90° , AB=10 cm,BC=6 cm,CD⊥AB交 AB于点 D.求: (1)AC的长; (2)△ABC的面积; (3)CD 的长. 11. 如图,在由边长为1 个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为 ( ) A.5 B.6 C.7 D.25 12. 如图,△ ABC和△ DCE都是边长为 4 的等边三角形,点 B、C、E在同一条直线上,连接BD,则BD的长为 ( ) A.3 B.23 C.33 D.4313. 将一个有 45 度角的三角板的直角顶点放在一张宽为3 cm的纸带边沿上 , 另一个顶点在纸带的另一边沿上 , 测得三角板的一边与纸带的一边所在的直线成30 度角 , 如图 , 则三角板的最大边的长为( ) A.3 cm B.6 cm C.32 cm D.62 cm 14. 如图,在直线 l 上依次摆放着三个正方形, 已知中间斜放置的正方形的面积...