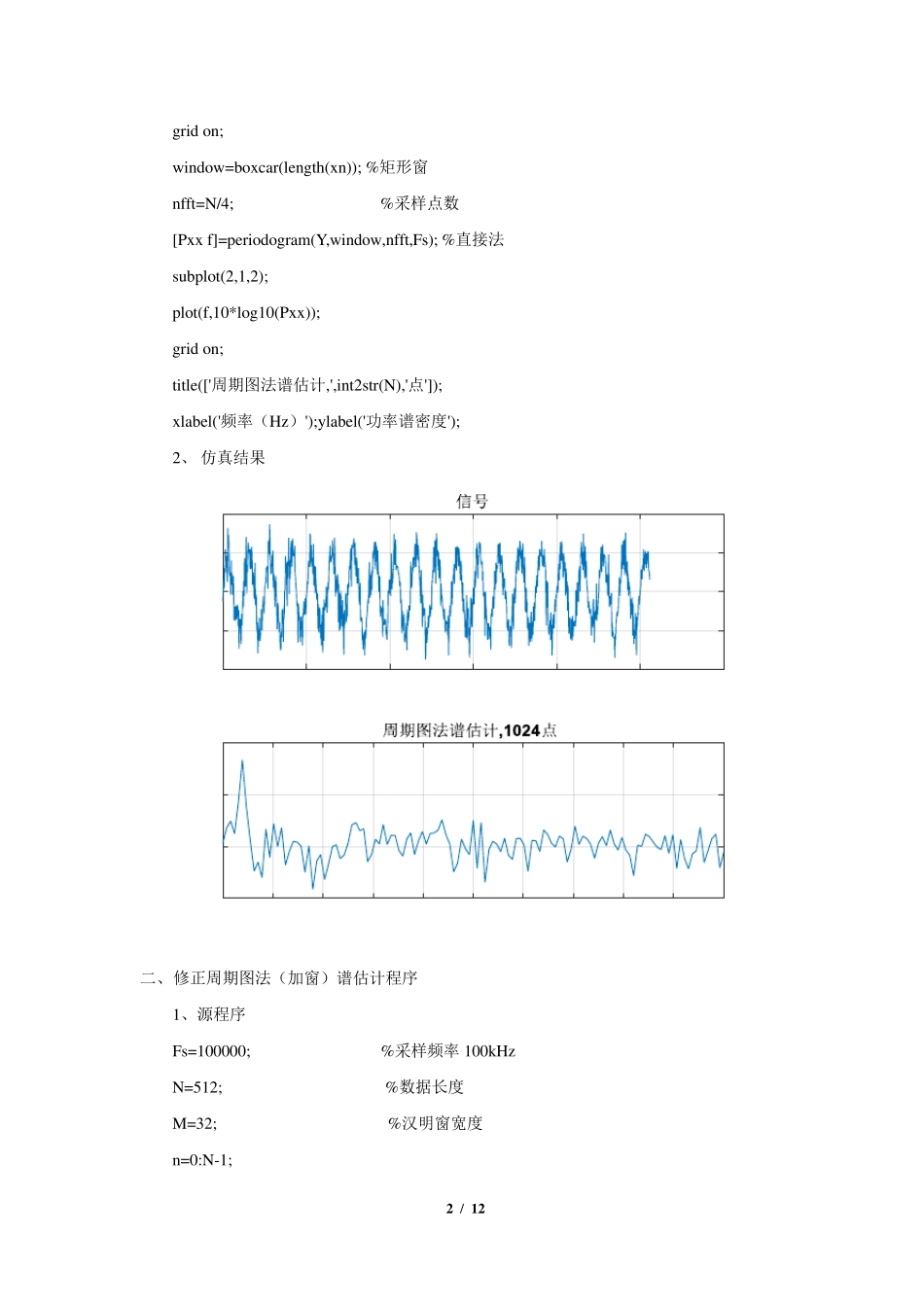
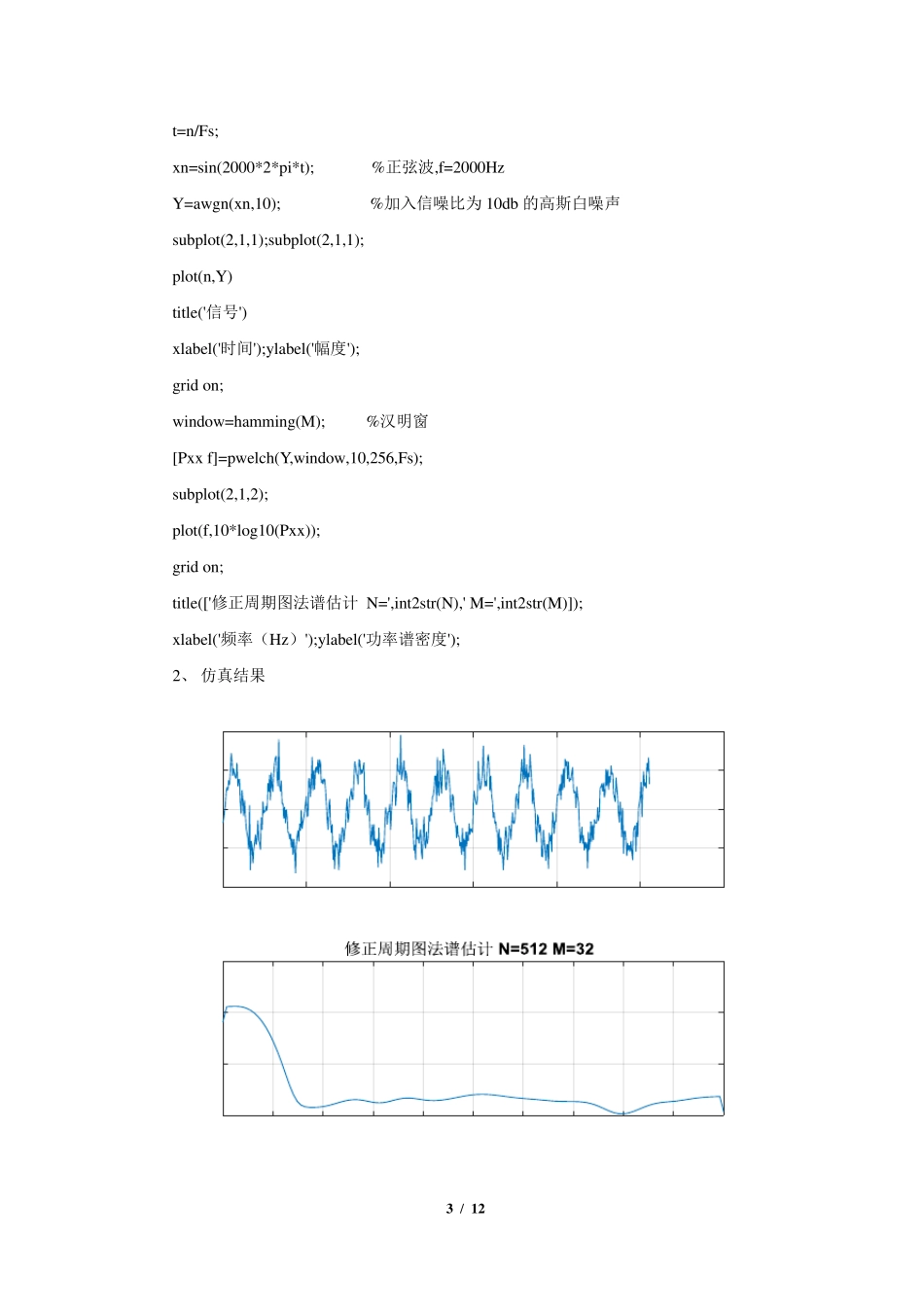
1 / 12 功率谱密度估计方法的 MATLAB 实现 在应用数学和物理学中,谱密度、功率谱密度和能量谱密度是一个用于信号的通用概念,它表示每赫兹的功率、每赫兹的能量这样的物理量纲。在物理学中,信号通常是波的形式,例如电磁波、随机振动或者声波。当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率,这被称为信号的功率谱密度(power spectral density, PSD)或者谱功率分布(spectral power distribution, SPD)。功率谱密度的单位通常用每赫兹的瓦特数(W/Hz)表示,或者使用波长而不是频率,即每纳米的瓦特数(W/nm)来表示。信号的功率谱密度当且仅当信号是广义的平稳过程的时候才存在。如果信号不是平稳过程,那么自相关函数一定是两个变量的函数,这样就不存在功率谱密度,但是可以使用类似的技术估计时变谱密度。信号功率谱的概念和应用是电子工程的基础,尤其是在电子通信系统中,例如无线电和微波通信、雷达以及相关系统。因此学习如何进行功率谱密度估计十分重要,借助于 Matlab 工具可以实现各种谱估计方法的模拟仿真并输出结果。下面对周期图法、修 正 周期图法、最 大 熵 法、Levinson 递 推 法和Burg 法的功率谱密度估计方法进行程序 设 计及仿真并给 出仿真结果。 以下程序 运 行平台 : Matlab R2015a(8.5.0.197613) 一、 周期图法谱估计程序 1、 源 程序 Fs=100000; %采 样频率 100kHz N=1024; %数据 长度N=1024 n=0:N-1; t=n/Fs; xn=sin(2000*2*pi*t); %正 弦 波,f=2000Hz Y=awgn(xn,10); %加 入 信噪 比 为 10db 的高 斯 白 噪 声 subplot(2,1,1); plot(n,Y) title('信号') xlabel('时间 ');ylabel('幅 度'); 2 / 12 grid on; window=boxcar(length(xn)); %矩形窗 nfft=N/4; %采样点数 [Pxx f]=periodogram(Y,window,nfft,Fs); %直接法 subplot(2,1,2); plot(f,10*log10(Pxx)); grid on; title(['周期图法谱估计,',int2str(N),'点']); xlabel('频率(Hz)');ylabel('功率谱密度'); 2、 仿真结果 二、 修正周期图法(加窗)谱估计程序 1、源程序 Fs=100000; %采样频率100kHz N=512; %数据长度 M=32; %汉明窗宽度 n=0:N-1; 3 / 12 t=n/Fs; xn=sin(2000*2*pi*t); %正弦波,f=2000Hz Y=awgn(xn,10); %加入信噪比为10db 的高斯白噪声 subplot(2,1,1);subplot(2,1,1); plot(n,Y) title('信号') xlab...