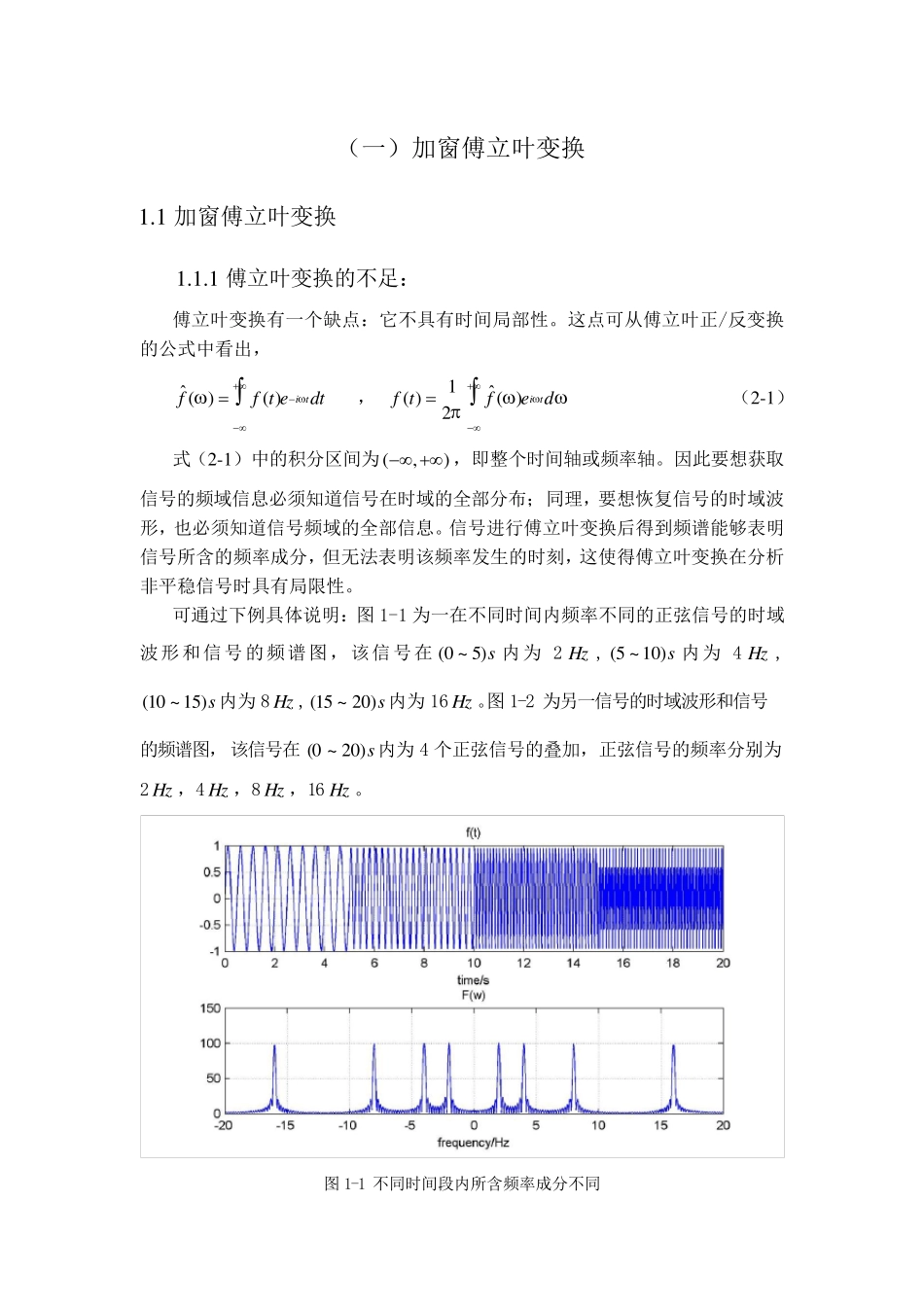
(一)加窗傅立叶变换 1.1 加窗傅立叶变换 1.1.1 傅立叶变换的不足: 傅立叶变换有一个缺点:它不具有时间局部性。这点可从傅立叶正/反变换的公式中看出, ˆ( )( )i tff t edt , 1ˆ( )( )2i tf tfe d (2-1) 式(2-1)中的积分区间为(,) ,即整个时间轴或频率轴。因此要想获取信号的频域信息必须知道信号在时域的全部分布;同理,要想恢复信号的时域波形,也必须知道信号频域的全部信息。信号进行傅立叶变换后得到频谱能够表明信号所含的频率成分,但无法表明该频率发生的时刻,这使得傅立叶变换在分析非平稳信号时具有局限性。 可通过下例具体说明:图 1-1 为一在不同时间内频率不同的正弦信号的时域波形和信号的频谱图,该信号在 (0 ~ 5)s 内为 2 Hz , (5 ~ 10)s 内为 4 Hz , (10 ~ 15)s 内为 8 Hz ,(15 ~ 20)s 内为 16 Hz 。图 1-2 为另一信号的时域波形和信号的频谱图,该信号在 (0 ~ 20)s 内为 4 个正弦信号的叠加,正弦信号的频率分别为2 Hz ,4 Hz ,8 Hz ,16 Hz 。 图 1-1 不同时间段内所含频率成分不同 图1-2 任意时间段含有4 种频率成分 从图1-1 和图1-2 可以看出,两信号在时域相差很大,但在频域上差别并不是非常明显,均在2 Hz,4 Hz,8 Hz,16 Hz处能量较强,而在其他频率处能量较低。仅从两者的频谱图,我们无法判断出信号的时域波形。 对于上例所示的简单信号,傅立叶变换都具有一定的局限性,更别说对于一些更为一般的信号了,如我们想分析一些音乐片段所包含的频率时,对信号做了傅立叶变换,得到了频谱,但从频谱上我们并不能判断出高频出现在什么时刻,低频出现在什么时刻,得到的频谱并不明显,在这种情况下,傅立叶变换的实际意义不大。 1.1.2 加窗傅立叶变换的定义 加窗傅立叶变换(WFT:Window ed Fourier Transform)也称短时傅立叶(STFT: Short Time Fourier Transform)或窗口傅立叶变换,是用一个在时间上有一定宽度的窗函数在时间轴上平移,并和待分析的信号相乘,然后再用傅立叶变换对相乘信号进行分析,得到该时刻附近对应信号的频谱。 WFT 的实现过程如下: ( )( ) ()tf uf u g ut ˆ( , )( )tftf 22( , )( )( ) ()i ui utftf u eduf u g ut edu (1-2) 实现过程也可用...