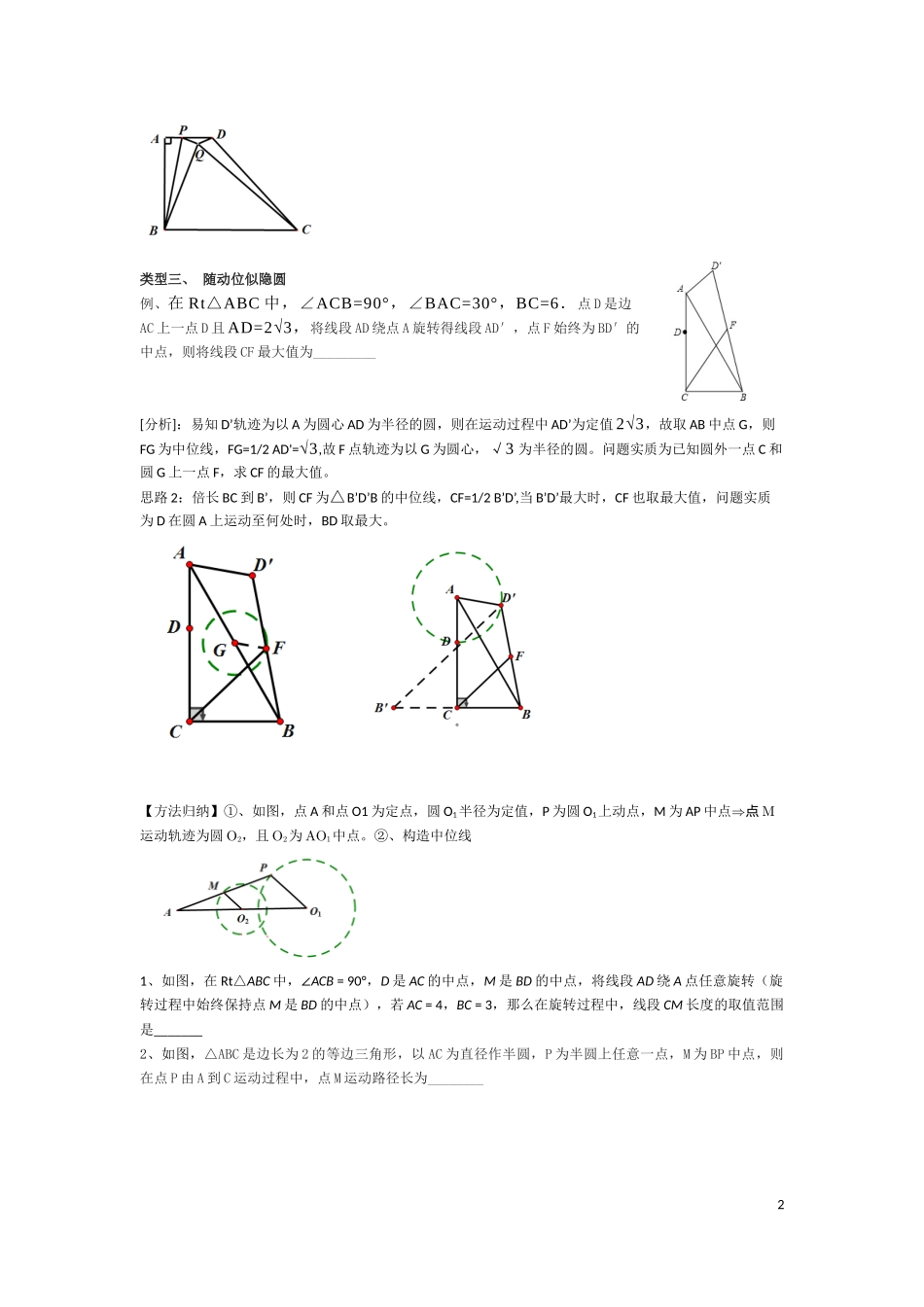
圆中最定值类型一、圆中将军饮马例 1、如图,AB 是⊙O 的直径,AB=10cm,M 是半圆 AB 的一个三等分点,N 是半圆 AB 的一个六等分点,P 是直径 AB 上一动点,连接 MP、NP,则 MP+NP 的最小值是_______1、已知圆 O 的面积为 3π,AB 为直径,弧 AC 的度数为 80 度,弧 BD 的度数为 20 度,点 P 为直径 AB 上任一点,则 PC+CD 的最小值为______2、如图,菱形 ABC 中,∠A=60 度,AB=3, 圆 A、圆 B 的半径为 2 和 1,P、E、F 分别是 CD,圆 A 和圆 B 上的动点,则 PE+PF 的最小值为_________ 类型二、折叠隐圆【基本原理】(一箭穿心)点 A 为圆外一点,P 为圆 O 上动点,连接 AO 并延长交圆于 P1、P2,则 AP 的最小值为 AP2,,最大值为 A P1例、如图 4,在边长为 2 的菱形 ABCD 中,∠A=60°,M 是 AD 边的中点,N 是 AB 边上一动点,将△AMN 沿 MN 所在的直线翻折得到△A′MN,连接 A′C,请求出 A′B 长度的最小值.1、已知一个矩形纸片 OACB,将该纸片放置在平面直角坐标洗中,点 A(11,0),点 B(0,6),点 P 为BC 边上的动点(点 P 不与点 B、C 重合),经过点 O、P 折叠该纸片,则 CB’的最小值为______2、四边形 ABCD 中,AD∥BC,∠A=90,AD=1,AB=2,BC=3,P 是线段 AD 上一动点,将△ABP 沿 BP 所在直线翻折得到△QBP,则△CQD 的面积最小值为____1类型三、 随动位似隐圆例、在 Rt△ABC 中,∠ACB=90°,∠BAC=30°,BC=6.点 D 是边AC 上一点 D 且 AD=2√3,将线段 AD 绕点 A 旋转得线段 AD′,点 F 始终为 BD′的中点,则将线段 CF 最大值为_________[分析]:易知 D’轨迹为以 A 为圆心 AD 为半径的圆,则在运动过程中 AD’为定值 2√3,故取 AB 中点 G,则FG 为中位线,FG=1/2 AD'=√3,故 F 点轨迹为以 G 为圆心,√3 为半径的圆。问题实质为已知圆外一点 C 和圆 G 上一点 F,求 CF 的最大值。思路 2:倍长 BC 到 B’,则 CF 为△B’D’B 的中位线,CF=1/2 B’D’,当 B’D’最大时,CF 也取最大值,问题实质为 D 在圆 A 上运动至何处时,BD 取最大。 【方法归纳】①、如图,点 A 和点 O1 为定点,圆 O1半径为定值,P 为圆 O1上动点,M 为 AP 中点⇒点 M运动轨迹为圆 O2,且 O2为 AO1中点。②、构造中位线1、如图,在 Rt△ABC 中,∠ACB = 90°,...