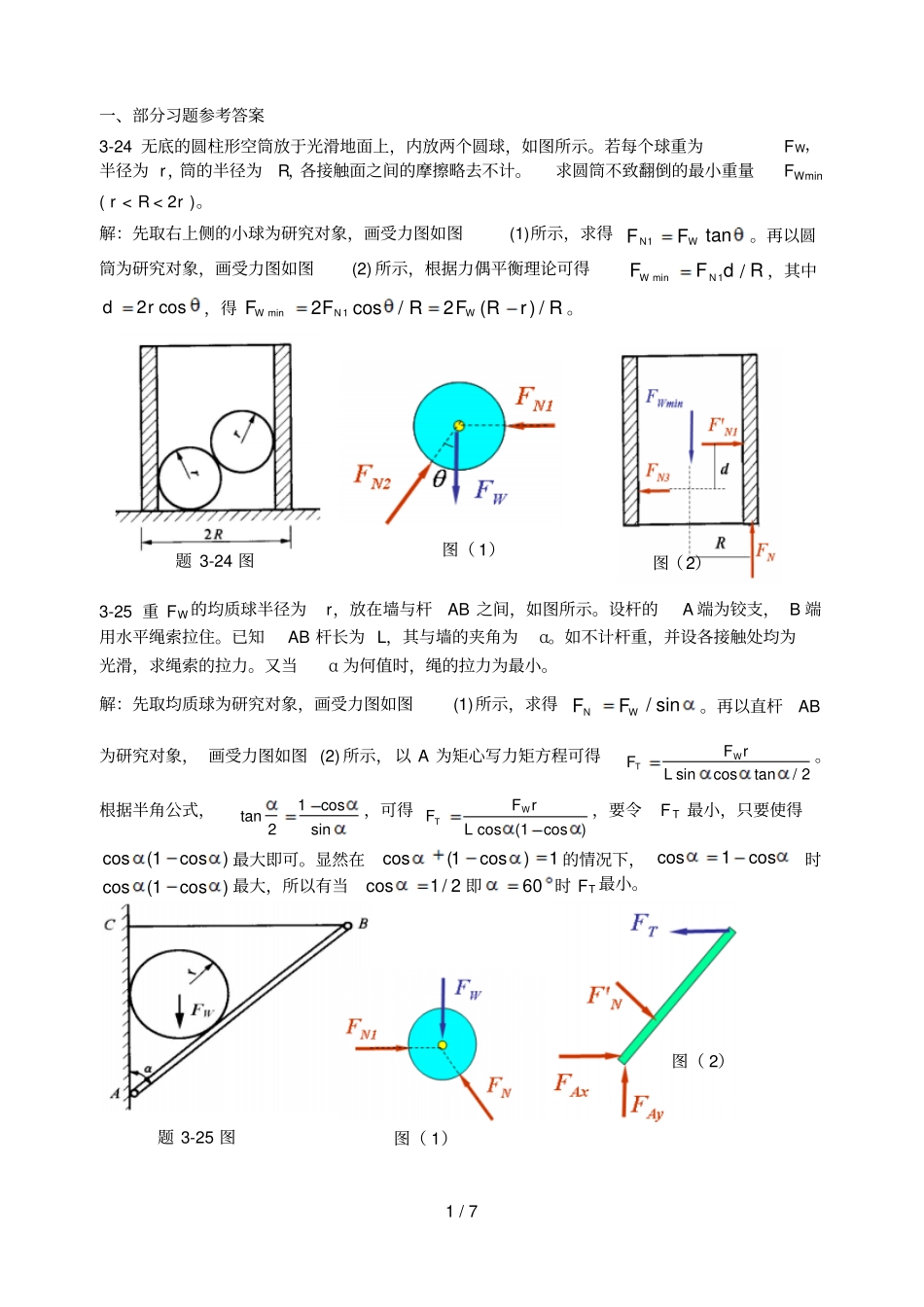
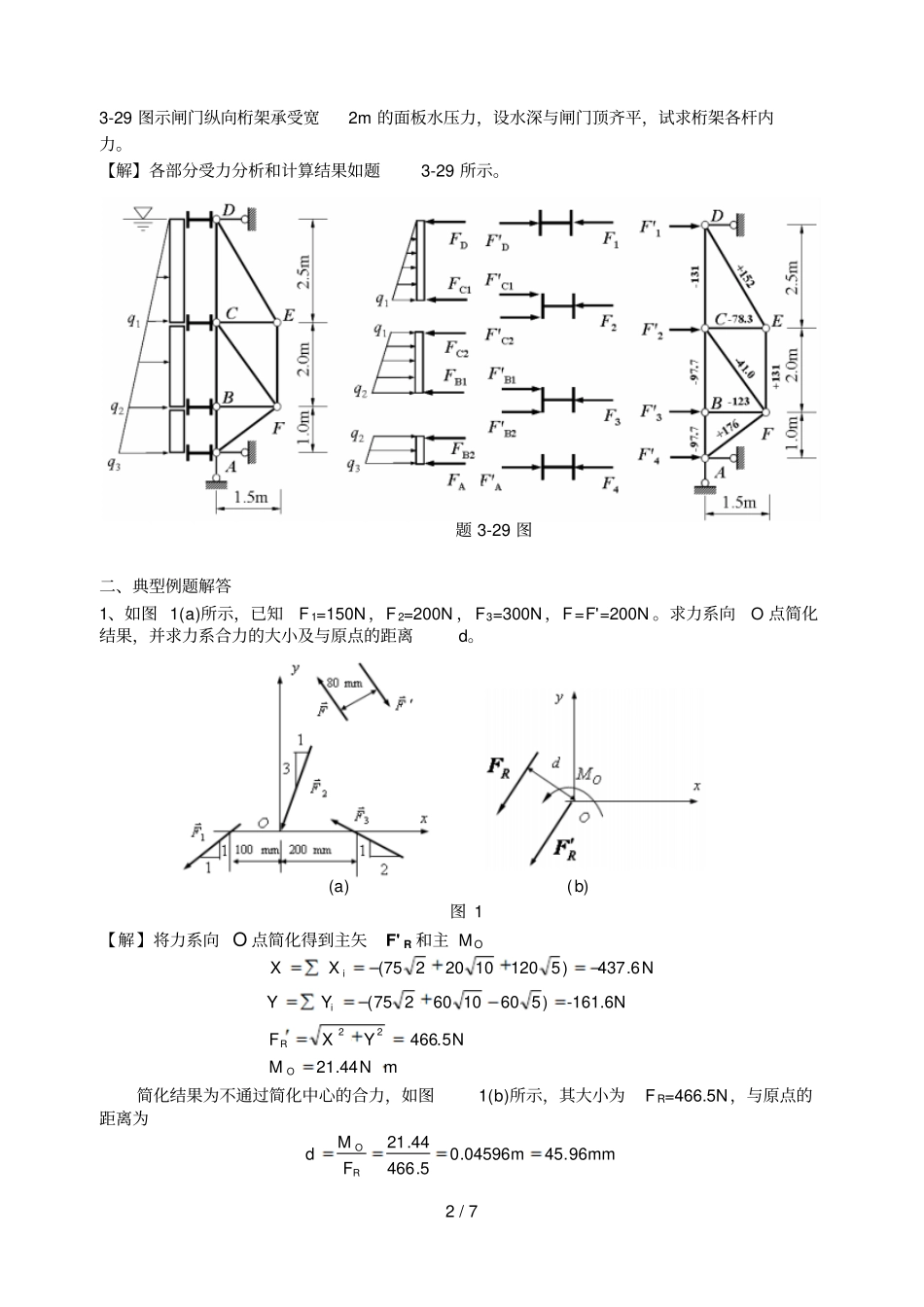
1 / 7 题 3-24 图一、部分习题参考答案3-24 无底的圆柱形空筒放于光滑地面上,内放两个圆球,如图所示。若每个球重为FW,半径为 r,筒的半径为R,各接触面之间的摩擦略去不计。求圆筒不致翻倒的最小重量FWmin ( r < R < 2r )。解:先取右上侧的小球为研究对象,画受力图如图(1)所示,求得tan1WNFF。再以圆筒为研究对象,画受力图如图(2) 所示,根据力偶平衡理论可得RdFFNW/1min,其中cos2rd,得RrRFRFFWNW/)(2/cos21min。3-25 重 FW 的均质球半径为r,放在墙与杆AB 之间,如图所示。设杆的A 端为铰支, B 端用水平绳索拉住。已知AB 杆长为 L,其与墙的夹角为α。如不计杆重,并设各接触处均为光滑,求绳索的拉力。又当α 为何值时,绳的拉力为最小。解:先取均质球为研究对象,画受力图如图(1)所示,求得sin/WNFF。再以直杆AB为研究对象, 画受力图如图 (2) 所示,以 A 为矩心写力矩方程可得2/tancossinLrFFWT。根据半角公式,sincos12tan,可得)cos1(cosLrFFWT,要令F T 最小,只要使得)cos1(cos最大即可。显然在1)cos1(cos的情况下,cos1cos时)cos1(cos最大,所以有当2/1cos即60 时 FT 最小。题 3-25 图图(2)图( 1)图( 1)图( 2)2 / 7 3-29 图示闸门纵向桁架承受宽2m 的面板水压力,设水深与闸门顶齐平,试求桁架各杆内力。【解】各部分受力分析和计算结果如题3-29 所示。二、典型例题解答1、如图 1(a)所示,已知F 1=150N ,F 2=200N ,F3=300N ,F=F'=200N 。求力系向O 点简化结果,并求力系合力的大小及与原点的距离d。【解】将力系向 O 点简化得到主矢F' R 和主 M OmN44.21N5.466-161.6N)5601060275(N6.437)51201020275(22ORiiMYXFYYXX简化结果为不通过简化中心的合力,如图1(b)所示,其大小为F R=466.5N,与原点的距离为mm96.45m04596.05.46644.21ROFMd题 3-29 图图 1 (b) (a) 3 / 7 2、图 2(a)所示构架中, 物体重 FP=1200N ,由细绳跨过滑轮E 而水平系于墙上, 尺寸如图,不计杆和滑轮的重量。求支承A 和 B 处的约束力,以及杆BC 的内力 F BC。【解】1)取整体为研究对象,画受力图如图2(a)所示,列平衡方程得0,0TAxiFFX,N1200AxF0)5.1()2(4,0rFrFFMTPBA,N1050BF0,0BPAyiFFFY,N150AyF2)取杆 ADB 为研究对象,画受力图如图2(b)所示,列平衡方程得022sin2,0AyBCBDFFFM,N1500BCF3、构架尺寸如图3(a)所示 (尺寸单位为m),不计各杆自重,荷...