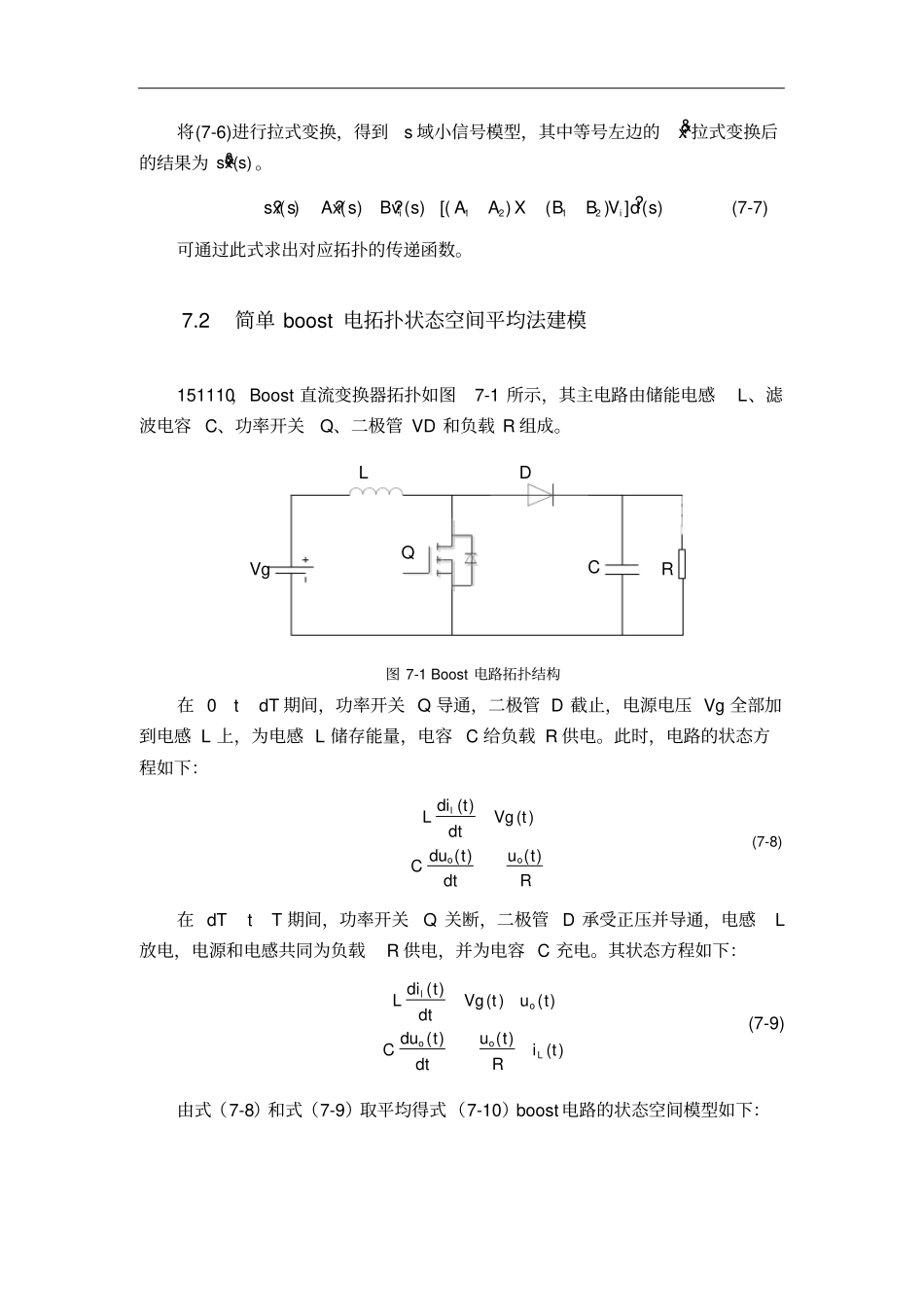
7.1 状态空间平均法151109,状态空间平均法是平均法的一阶近似,其实质为:根据线性 RLC元件、独立电源和周期性开关组成的原始网络,以电容电压、电感电流为状态变量,按照功率开关器件的“ ON”和“ OFF”两种状态,利用时间平均技术,得到一个周期内平均状态变量, 将一个非线性电路转变为一个等效的线性电路,建立状态空间平均模型。对于不考虑寄生参数的理想PWM 变换器,在连续工作模式(CCM)下一个开关周期有两个开关状态相对应的状态方程为:11 ixA xB v&0tdT(7-1)22ixA xB v&dTtT(7-2)式中 d 为功率开关管导通占空比,/ondtT ,ont为导通时间, T 为开关周期; vLCxi,x 是状态变量, x&是状态变量的导数,Li 是电感电流Cv 是电容电压,iV 是开关变换器的输入电压;1A ,2A ,1B ,2B 是系数矩阵与电路的结构参数有关。对式( 7.1)和( 7.2)进行平均得到状态平均方程为xAxBv&0tT(7-3)式中,12(1)AdAd A ,12(1)BdBd B ,这就是著名的状态空间平均法。可此式可见,时变电路变成了非时变电路,若d 为常数,则这个方程描述的系统是线性系统, 所以状态空间平均法的贡献是把一个开关电路用一个线性电路来替代。对状态平均方程进行小扰动线性化,令瞬时值?dDd 、'?'dDd 、'1DD、?vgVgvg 、?xXx 。其中 ?d 、 ?vg 、 ?x 是相应 D、 vg 、X 的扰动量,将之代入到式( 7-3)为:????()()iiXxA XxB Vv&(7-4) ''1212????????()()()()()()iiiA XxB VvAxBxDd ADd AXDd BDd BV(7-5) 将其中的扰动参数变量分离就得到了动态的小信号模型式。1212????[()()]iixAxBvAAXBB V d&(7-6) 将(7-6)进行拉式变换,得到s 域小信号模型,其中等号左边的?x&拉式变换后的结果为?sx(s)&。1212????( )( )( )[()()] ( )iisx sAx sBv sAAXBB V d s(7-7)可通过此式求出对应拓扑的传递函数。7.2 简单 boost 电拓扑状态空间平均法建模151110,Boost 直流变换器拓扑如图7-1 所示,其主电路由储能电感L、滤波电容 C、功率开关Q、二极管 VD 和负载 R 组成。CRLQDVg图 7-1 Boost 电路拓扑结构在 0tdT 期间,功率开关 Q 导通,二极管 D 截止,电源电压 Vg 全部加到电感 L 上,为电感 L 储存能量,电容 C 给负载 R 供电。此时,电路的状态方程如下:( )( )( )( )looditLVg tdtdututCdtR(7-8) 在 dTtT 期间,功率开关Q 关断,二极管 D 承受正压并导通,电感L放电,...