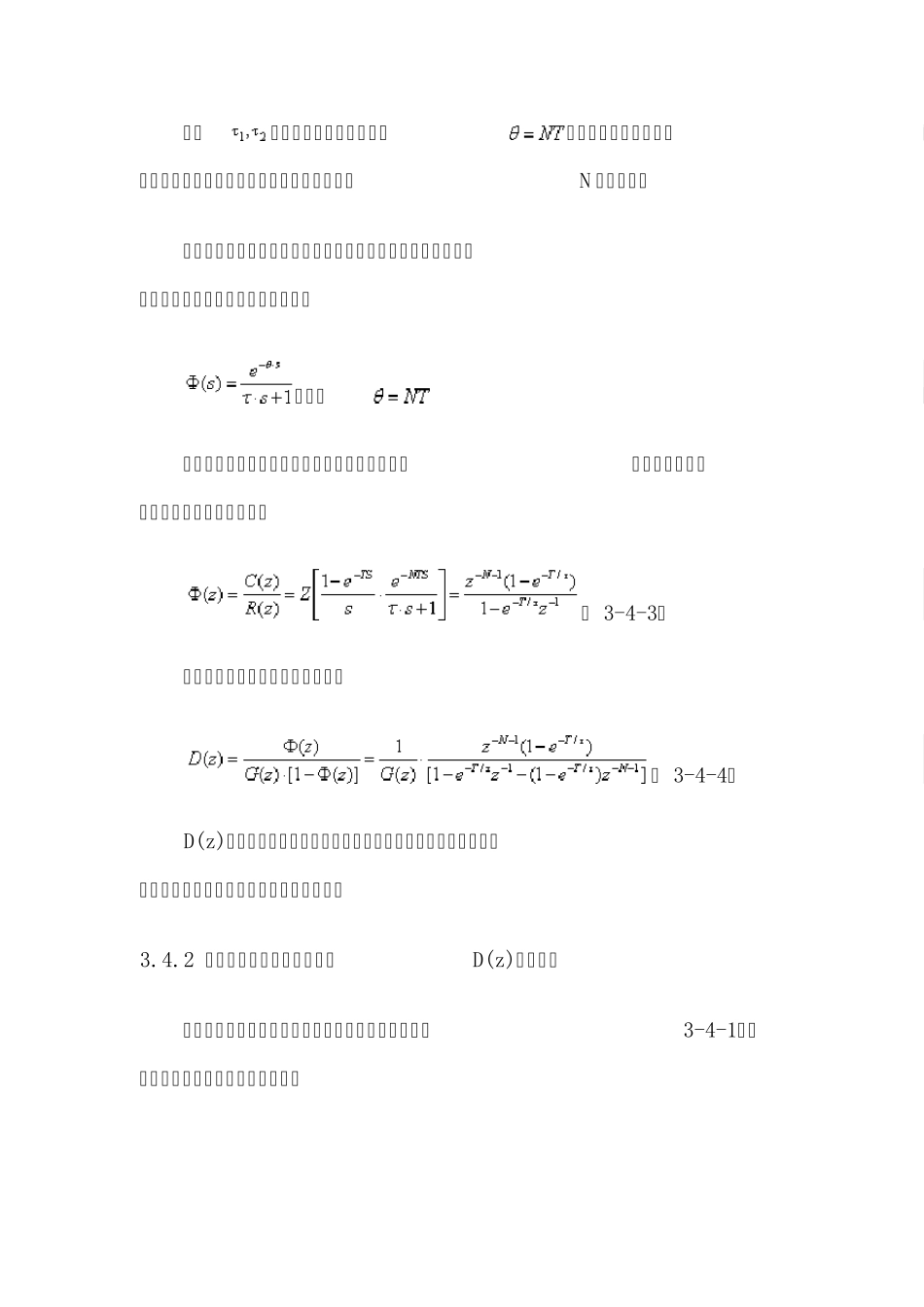
3.4 大林(Dahlin)算法 前面介绍的最少拍无纹波系统的数字控制器的设计方法只适合于某些随动系统,对系统输出的超调量有严格限制的控制系统它并不理想。在一些实际工程中,经常遇到纯滞后调节系统,它们的滞后时间比较长。对于这样的系统,往往允许系统存在适当的超调量,以尽可能地缩短调节时间。人们更感兴趣的是要求系统没有超调量或只有很小超调量,而调节时间则允许在较多的采样周期内结束。也就是说,超调是主要设计指标。对于这样的系统,用一般的随动系统设计方法是不行的,用PID 算法效果也欠佳。 针对这一要求,IBM 公司的大林(Dahlin)在 1968 年提出了一种针对工业生产过程中含有纯滞后对象的控制算法。其目标就是使整个闭环系统的传递函数 相当于一个带有纯滞后的一阶惯性环节。该算法具有良好的控制效果。 3.4.1 大林算法中D(z)的基本形式 设被控对象为带有纯滞后的一阶惯性环节或二阶惯性环节,其传递函数分别为: ( 3-4-1) ( 3-4-2) 其中为被控对象的时间常数,为被控对象的纯延迟时间,为了简化,设其为采样周期的整数倍,即N 为正整数。 由于大林算法的设计目标是使整个闭环系统的传递函数相当于一个带有纯滞后的一阶惯性环节,即 ,其中 由于一般控制对象均与一个零阶保持器相串联,所以相应的整个闭环系统的脉冲传递函数是 ( 3-4-3) 于是数字控制器的脉冲传递函数为 ( 3-4-4) D(z)可由计算机程序实现。由上式可知,它与被控对象有关。下面分别对一阶或二阶纯滞后环节进行讨论。 3.4.2 一阶惯性环节的大林算法的D(z)基本形式 当被控对象是带有纯滞后的一阶惯性环节时,由式(3-4-1)的传递函数可知,其脉冲传递函数为 将此式代入(3-4-4),可得 ( 3-4-5) 式中:T——采样周期: ———被控对象的时间常数; ———闭环系统的时间常数。 3.4.3 二阶惯性环节大林算法的D(z)基本形式 当被控对象为带有纯滞后的二阶惯性环节时,由式(3-4-1)的传递函数可知,其脉冲传递函数为 其中, 将式G(z)代入式(3-4-3)即可求出数字控制器的模型: ( 3-4-6) 3.4.4 振铃现象及其消除方法 振铃现象是指数字控制器的输出以接近1/2 采样频率的频率,大幅度衰减振荡。它对系统的输出几乎无影响,但会使执行机构因磨损而造成损坏。 衡量振铃现象的强烈程度的量是振铃幅度RA (Ringing Amplitude)。它的定义是:控制器在单位阶跃输入作用下,第零次输出幅度与第一次输出幅度之差值。...