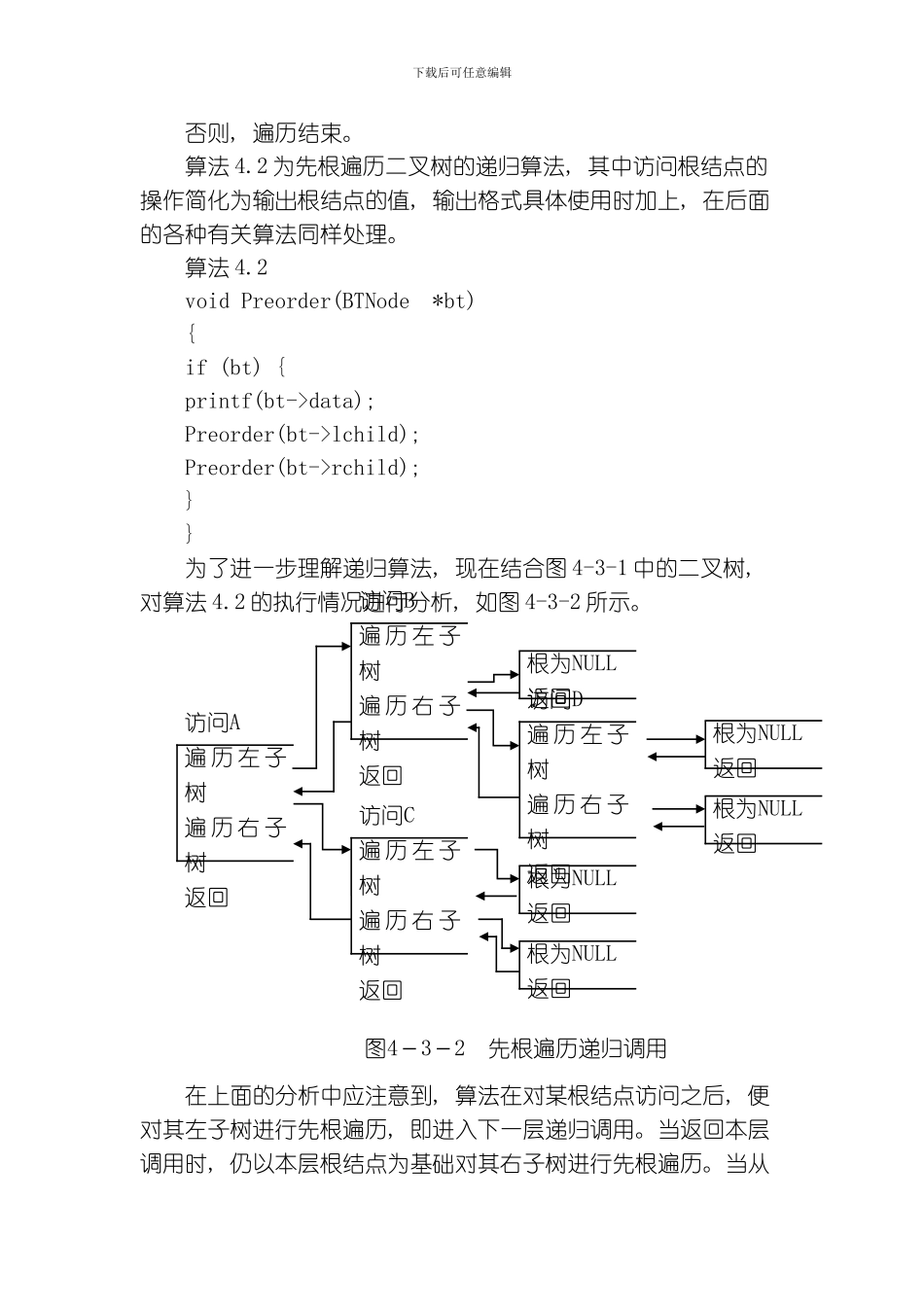
下载后可任意编辑1.熟练掌握各种遍历策略的递归和非递归算法。2.. 熟练掌握二叉树的线索化过程以及在中序线索化树上找给定结点的前驱和后继的方法。。 教学重点: 掌握二叉树的遍历, 包括中根遍历、 前根遍历和后根遍历方法。 教学难点: 理解什么是线索, 中序线索化二叉树的结构特性及寻找某结点的前驱和后继的方法。 授课内容4.3 遍历二叉树遍历二叉树是指以某种顺序访问二叉树中的每个结点, 而且每个结点仅被访问一次。这里”访问”的含义很广, 能够是查询结点数据域的内容、 输出结点的数据、 修改结点的数据或是执行对结点的其它操作。假设遍历时访问结点仅是输出结点数据域的值, 那么遍历的结果将是得到一个线性序列。由于二叉树有左、 右子树, 因此遍历的次序不同, 得到的结果就会不同。假设 L、 T、 R 分别代表遍历左子树、 访问根结点和遍历右子树, 则对一棵二叉树的遍历能够有六种不同次序: TLR、 LTR、 LRT、 TRL、 RTL、 RTL。若约定先左( L)后右( R) , 再把访问根结点( T) 穿插其中, 则只有三种不同的遍历次序: TLR、 LTR 和 LRT。它们分别称作先根遍历、 中根遍历和后根遍历。 在介绍常见的三种遍历算法之前, 先介绍一下遍历的具体方第十三讲 二叉树下载后可任意编辑法。例如有一棵二叉树, 它有四个结点。为了便于理解遍历的思想, 临时为每个没有子树的结点均补充上相应的空子树, 用 ø 表示, 见图 4-3-1。设想有一条搜索路线( 用虚线表示) , 它从根结点的左支开始, 自上而下自左至右搜索, 最后由根结点右支向上出去。不难看出, 若考虑到空子树的话, 恰好搜索线途径每个有效结点都是三次。把第一次经过就访问的结点列出, 它们是 A、 B、 D、 C, 这就是先根遍历的结果。那么第二此经过才访问的则是中根遍历, 其结果是 B、 D、 A、 C。第三次经过才访问的是后根遍历, 结果是 D、 B、 C、 A。下面介绍三种遍历算法, 在算法中将采纳二叉链表作为二叉树的存储结构。4.3.1 先根遍历先根遍历的递归定义为: 若二叉树非空, 则( 1) 访问根结点; ( 2) 按先根次序遍历左子树; ( 3) 按先根次序遍历右子树。EB CA图4-3-1 遍历搜索示意图下载后可任意编辑否则, 遍历结束。算法 4.2 为先根遍历二叉树的递归算法, 其中访问根结点的操作简化为输出根结点的值, 输出格式具体使用时加上, 在后面的各种有关算法同样处理。算法 4.2void Preorder...