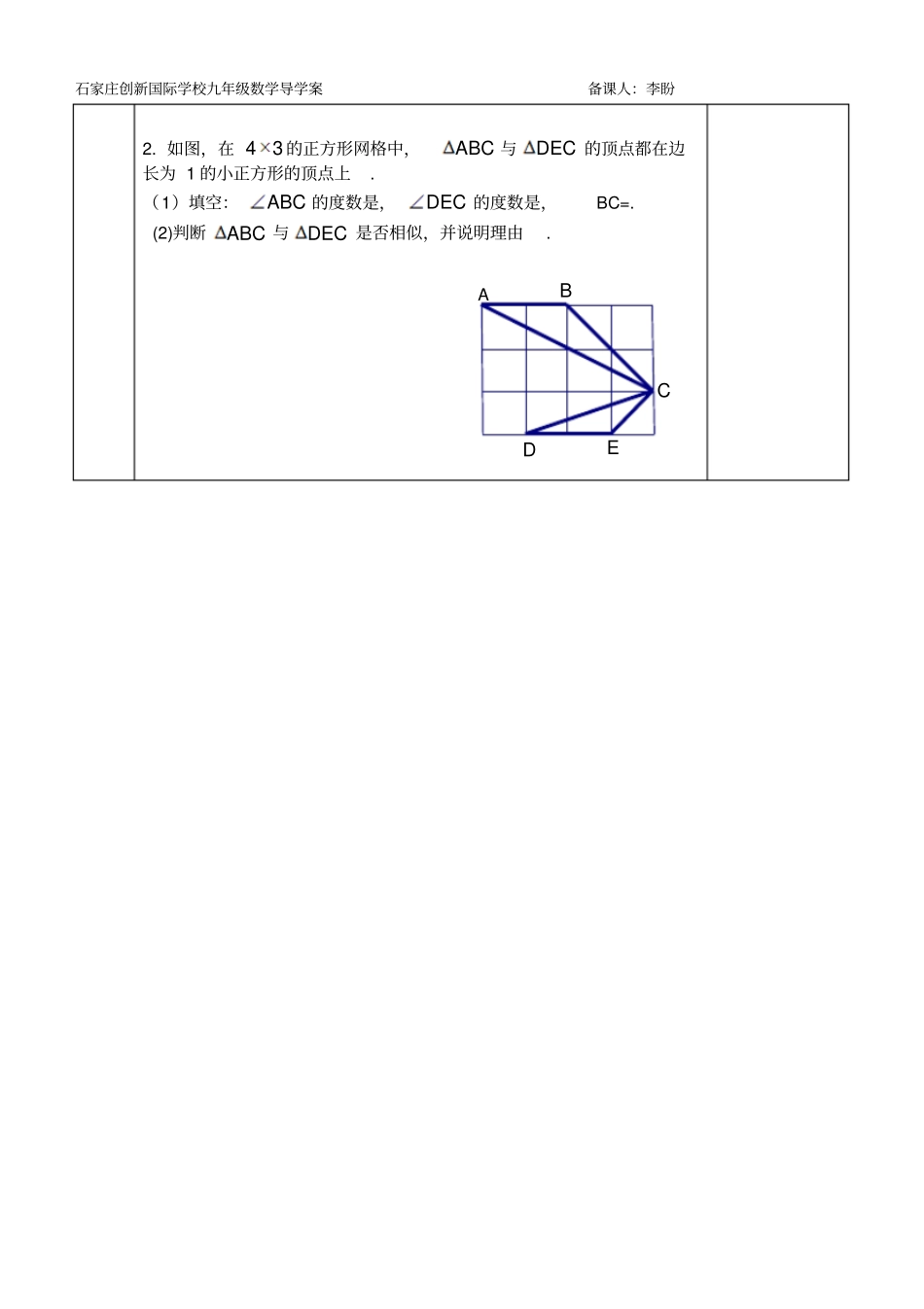
石家庄创新国际学校九年级数学导学案备课人:李盼C'B'A'CBA课题相似三角形的判定使用班级九年级 1-6 班课型预习展示上课时间11 月 27 日备课时间11 月 26 日环节活动 5min 解读目标: 2min 研学: 13min 展示: 15min 独学: 7min 检测 3min 目标能探究并会应用三条边对应成比例的两个三角形是相似三角形。学法指导教学内容活动对子组两个人合作画出两个三角形要求:使其中一个三角形的三边长是另一个三角形三边长的2 倍。问题发现:对子组将两个三角形进行比对,观察两个三角形是否相似?三边关系:三对角的关系:两个三角形是否相似:猜想: 三条边对应成比例的两个三角形根据你的猜想命题证明:如图:在'''ABCA B C和中,''''''ABBCACA BB CAC. 求证:ABC ∽'''A B C . 证明:在 AB 上截取 AE=A’B’过点 E 作 EF∥BC,交 AC于点 F 相似三角形判定定理:提示:纸张最好是透明的,画出的三角形痕迹深一些;你可以利用相似三角形的定义或已学过的判 定 方 法 进行。提 示 : 在 △ABC中截取一个三角形, 使得 这 个 三 角形与△ ABC相似又与'''A B C全等。石家庄创新国际学校九年级数学导学案备课人:李盼定理的应用:1、 已知:如图,在Rt △ ABC 与 Rt △ DEF 中,∠ B=∠ D=90° ,ABACDEDF.求证: Rt△ABC∽Rt△DEF 直角三角形相似的判定定理:小试牛刀:1. △ ABC 的三边AB=5cm, AC=10cm, BC=12cm,△ A’B’C’的三边A’B’=3cm,A’C’=6cm,B’C’=7.2cm。判断△ ABC与△ A’B’C’是否相似①可以利用三边成比例,但是已知条件缺少一条边成比例,而已学过的勾股定理能够将三边建立联系②根据我们刚刚学过的办法是否可以证出?③通过本题你能联想到相似三角形与全等三角形之间的联系吗?说一说。在以后解决问题时,此定理可以直接应用!△ABC与△A’B’ C’相似,点 A 与 A’不一定是对应点;而△ ABC∽△A’B’C’,则点 A与 A’一定是对应点ABCDEF石家庄创新国际学校九年级数学导学案备课人:李盼EDCBA2. 如图,在 43 的正方形网格中,ABC 与DEC 的顶点都在边长为 1 的小正方形的顶点上.(1)填空:ABC 的度数是,DEC 的度数是,BC=. (2)判断ABC 与DEC 是否相似,并说明理由. 石家庄创新国际学校九年级数学导学案备课人:李盼检测题已知△ ABC的三边长分别为6cm,7.5cm,9cm,△ DEF的一边长为4cm,当△ DEF的另两边长是下列哪一组时,△ABC能与△ DEF相似()A. 2cm,3cm B. 4cm,5cm C. 5cm,6cm D. 6cm,7cm检测题已知△ ABC的三边长分别为6cm,7.5cm,9cm,△ DEF的一边长为4cm,当△ DEF的另两边长是下列哪一组时,△ABC能与△ DEF相似()A. 2cm,3cm B. 4cm,5cm C. 5cm,6cm D. 6cm,7cm