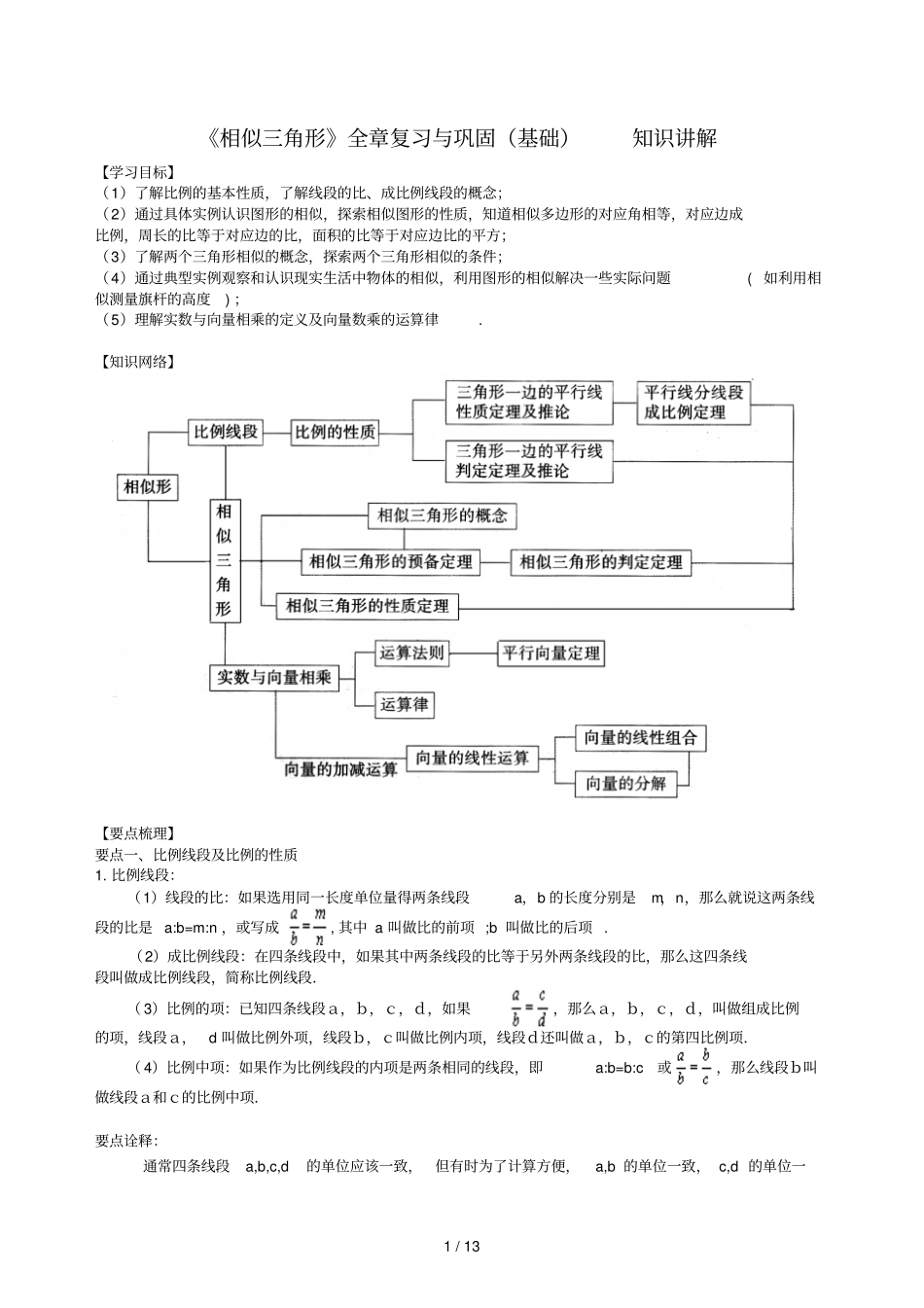
1 / 13 《相似三角形》全章复习与巩固(基础)知识讲解【学习目标】(1)了解比例的基本性质,了解线段的比、成比例线段的概念;(2)通过具体实例认识图形的相似,探索相似图形的性质,知道相似多边形的对应角相等,对应边成比例,周长的比等于对应边的比,面积的比等于对应边比的平方;(3)了解两个三角形相似的概念,探索两个三角形相似的条件;(4)通过典型实例观察和认识现实生活中物体的相似,利用图形的相似解决一些实际问题( 如利用相似测量旗杆的高度) ;(5)理解实数与向量相乘的定义及向量数乘的运算律. 【知识网络】【要点梳理】要点一、比例线段及比例的性质1. 比例线段:(1)线段的比:如果选用同一长度单位量得两条线段a,b 的长度分别是m,n,那么就说这两条线段的比是 a:b=m:n ,或写成, 其中 a 叫做比的前项 ;b 叫做比的后项 . (2)成比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.( 3)比例的项:已知四条线段a,b,c,d,如果,那么a,b,c,d,叫做组成比例的项,线段a,d 叫做比例外项,线段b,c叫做比例内项,线段d还叫做a,b,c的第四比例项.( 4)比例中项:如果作为比例线段的内项是两条相同的线段,即a:b=b:c或,那么线段b叫做线段a和c的比例中项.要点诠释:通常四条线段a,b,c,d的单位应该一致,但有时为了计算方便,a,b 的单位一致, c,d 的单位一2 / 13 致也可以 . 2. 比例的性质(1) 比例的基本性质:(2) 反比性质:(3) 更比性质 : 或(4) 合比性质 : (5) 等比性质 : 且3. 平行线分线段成比例定理(1)三角形一边的平行线性质定理: 平行于三角形一边的直线截其他两边( 或两边的延长线) 所得的对应线段成比例. (2)三角形一边的平行线性质定理推论: 平行于三角形一边并且和其他两边相交的直线, 所截得的三角形的三边与原三角形三边的对应成比例. (3)三角形一边的平行线判定定理:如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边. (4)三角形一边的平行线判定定理推论:如果一条直线截三角形两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.(5)平行线分线段成比例定理:两条直线被三条平行的直线所截,截得的对应线段成比例. (6)平行线等分线段定理:两条直线被三...