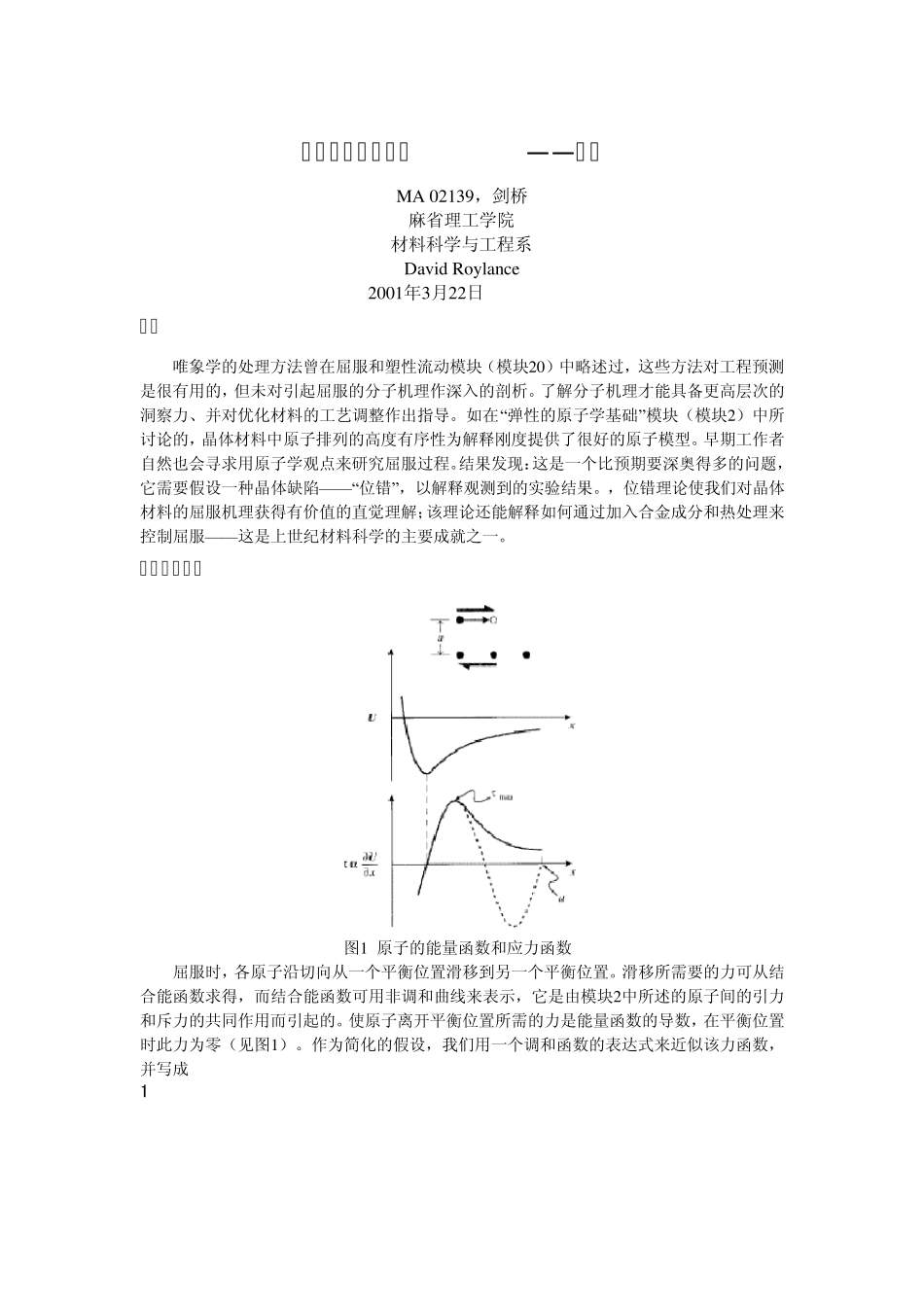
屈服和蠕变的基础——位错 MA 02139,剑桥 麻省理工学院 材料科学与工程系 Dav id Ro y lan ce 2001年3月22日 引言 唯象学的处理方法曾在屈服和塑性流动模块(模块20)中略述过,这些方法对工程预测是很有用的,但未对引起屈服的分子机理作深入的剖析。了解分子机理才能具备更高层次的洞察力、并对优化材料的工艺调整作出指导。如在“弹性的原子学基础” 模块(模块2)中所讨论的,晶体材料中原子排列的高度有序性为解释刚度提供了很好的原子模型。早期工作者自然也会寻求用原子学观点来研究屈服过程。结果发现:这是一个比预期要深奥得多的问题,它需要假设一种晶体缺陷— — “位错” ,以解释观测到的实验结果。,位错理论使我们对晶体材料的屈服机理获得有价值的直觉理解;该理论还能解释如何通过加入合金成分和热处理来控制屈服— — 这是上世纪材料科学的主要成就之一。 理论屈服强度 图1 原子的能量函数和应力函数 屈服时,各原子沿切向从一个平衡位置滑移到另一个平衡位置。滑移所需要的力可从结合能函数求得,而结合能函数可用非调和曲线来表示,它是由模块2中所述的原子间的引力和斥力的共同作用而引起的。使原子离开平衡位置所需的力是能量函数的导数,在平衡位置时此力为零(见图1)。作为简化的假设,我们用一个调和函数的表达式来近似该力函数,并写成 1 式中,a为原子的间距。在间距的四分之一处,应力达到最大值;在间距中点的亚稳定位置,应力降为零。过中点之后,应力改变符号,即力将阻挠原子朝新平衡位置的运动。以ax=γ为切应变,最大切应力maxτ与切变模量G的关系为 上式表明:屈服时的切应力102maxGG≈=πτ,此值在10GPa的量级。而maxτ的各测量值为10-100MPa,因此理论值大了二到三个量级。更精确的推导能得出略小的理论屈服应力值,但仍然比实验观察值大得多。 刃型位错、螺型位错和混合位错 对于晶体材料,其屈服强度的实验值相对理论值明显偏低,对该现象的解释分别由泰勒(Taylor)、普兰尼(Polyani)和奥罗万(Orowan)在1934 年独立提出。他们认识到:要使材料发生塑性变形,并不需要整个原子面在另一个原子面上滑移(即同时切断连接原子面的所有键)。要切断所有键,所需的应力将很大,如上所述在10G的量级。但实际上并不需要同时移动所有原子,仅需每次移动少量原子,故所需的应力要小得多。与尺蠖(一种昆虫)的移动相类似,仅某一位错线上方一个平面内的各原子要移动一个原子间...