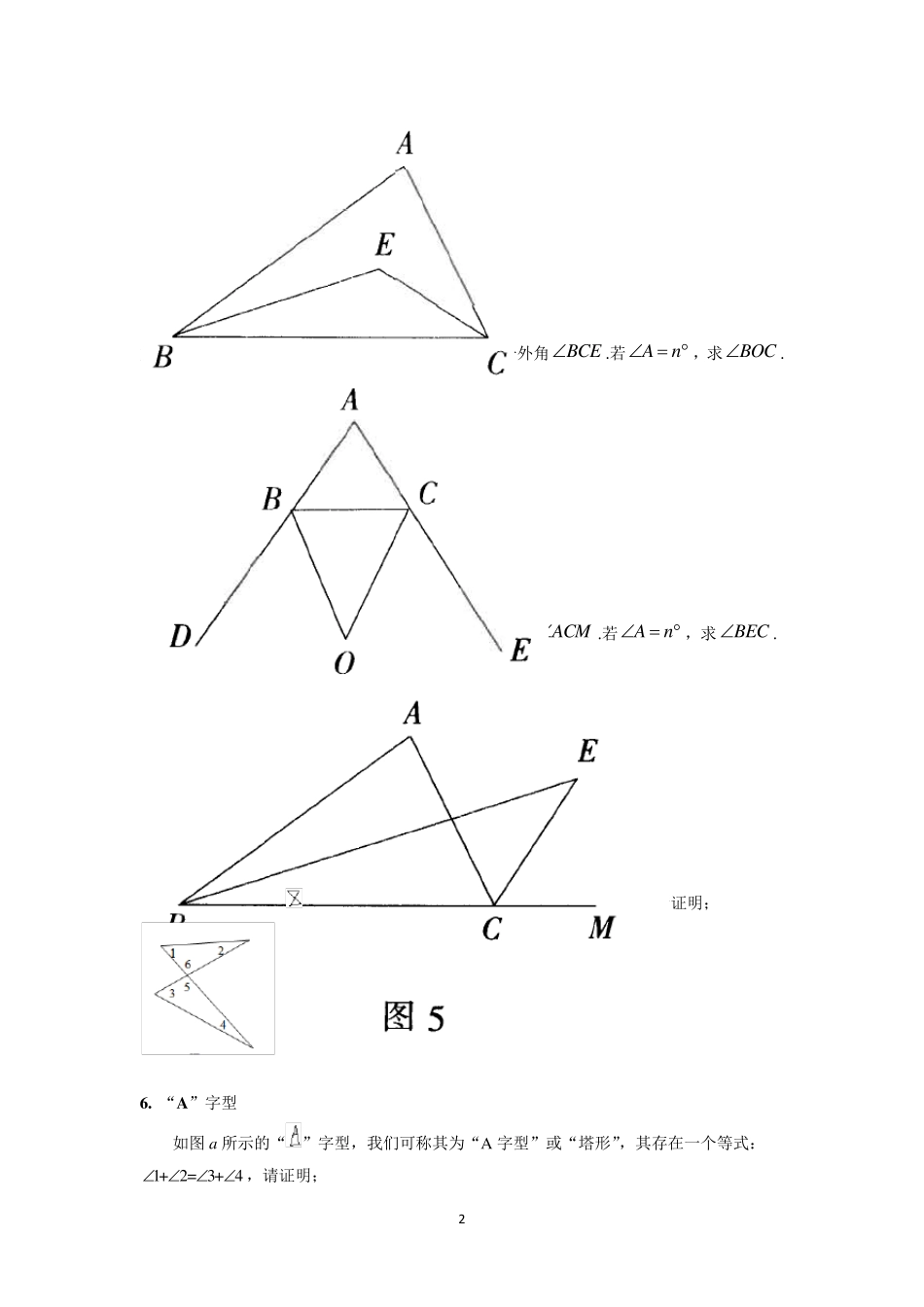
1 直 线 平 行 的 条 件和性质 1. 猪蹄模型 已知:如图,AB∥CD,求证:∠B+∠D=∠BED。 2. 铅笔模型 如图,已知: CDAB∥,求证: ∠B∠D +∠BED360°. (至少用三种方法) 3. 其他 4. 角平分线 如图1,在 ABC中, BE 平分,ABC CE平分ACB.若8 0A ,则BEC= ;若An ,求BEC用含 n的代数式表示) 2 如图3,在ABC中,BO平分外角 ,CBD CO平分外角BCE.若An ,求BOC. 如图5,在ABC中,BE 平分ABC, CE 平分外角ACM.若An ,求BEC. 5. “8”字形 如图b所示的“”字型,其也存在着一个等式: 1+ 2= 3+ 4 ,请证明; 6. “A ”字型 如图a所示的“”字型,我们可称其为“A 字型”或“塔形”,其存在一个等式:1+ 2= 3+ 4 ,请证明; 3 7 . 燕尾形 如图c所示,其也存在着如下等式:DABC ,请证明 一.考点:平行线的性质,角度的计算与证明. 二.重难点:常见的几种两条直线平行的结论 1.两条平行线被第三条直线所截,一组同位角的角平分线平行; 2.两条平行线被第三条直线所截,一组内错角的角平分线平行; 3.两条平行线被第三条直线所截,一组同旁内角的角平分线垂直. 三.易错点: 1.性质是由图形的“位置关系”决定“数量关系”; 2.两条平行线之间的距离其实可看成点到直线的距离. 题型一:猪蹄模型 例1. 如图,直线a∥b,直角三角形ABC 的顶点B 在直线a 上,∠C=90°,∠β=55°,则∠α的度数为( ) A. 15° B. 25° C. 35° D. 55° 题型二:铅笔模型 例2 . 如图,AB∥CD,AEFC ( ) 4 A. 180° B. 360° C. 540° D. 720° 题型三:铅笔、猪蹄模型综合压轴 例3. 某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题: 已知直线AB∥CD,点E 在AB、CD 之间,点P、Q 分别在直线AB、CD 上,连接PE、EQ. (1)如图1,运用上述结论,探究∠PEQ 与∠APE+∠CQE 之间的数量关系,并说明理由; (2)如图2,PF 平分∠BPE,QF 平分∠EQD,当∠PEQ=140°时,求出∠PFQ 的度数; (3)如图3,若点E 在CD 的下方,PF 平分∠BPE,QH 平分∠EQD,QH 的反向延长线交 PF于点F.当∠PEQ=70°时,请求出∠PFQ 的度数. 题型...