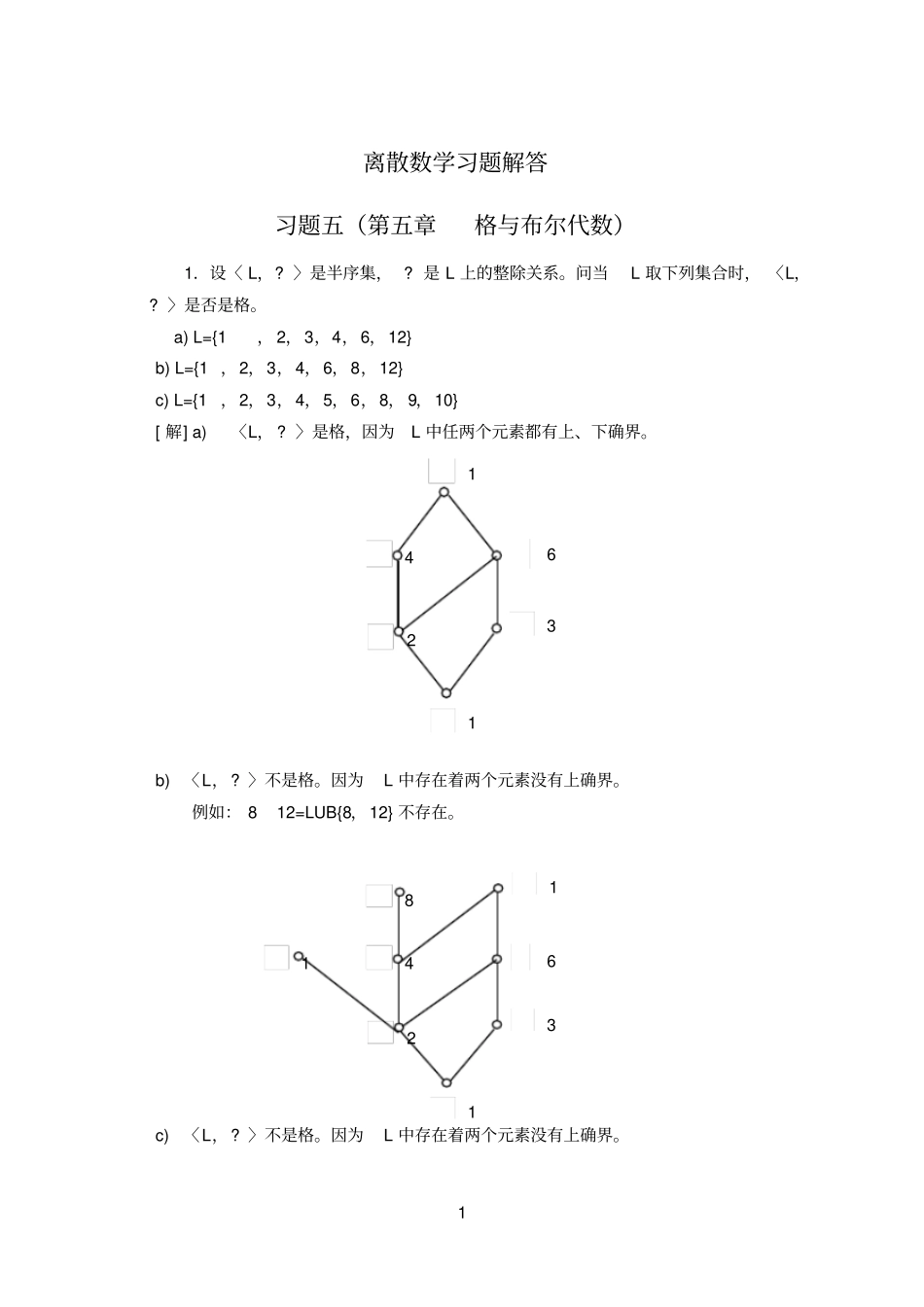
1 离散数学习题解答习题五(第五章格与布尔代数)1.设〈 L,? 〉是半序集, ? 是 L 上的整除关系。问当L 取下列集合时, 〈L,? 〉是否是格。 a) L={1, 2,3,4,6,12}b) L={1 ,2,3,4,6,8,12}c) L={1 ,2,3,4,5,6,8, 9,10}[ 解] a) 〈L, ? 〉是格,因为L 中任两个元素都有上、下确界。b) 〈L,? 〉不是格。因为L 中存在着两个元素没有上确界。例如: 812=LUB{8,12} 不存在。c) 〈L,? 〉不是格。因为L 中存在着两个元素没有上确界。163124863124112 倒例如: 46=LUB{4,6} 不存在。2.设 A,B 是两个集合, f 是从 A 到 B 的映射。证明: 〈S,? 〉是〈 2B,? 〉的子格。其中S={y|y=f (x),x∈2A}[ 证] 对于任何B1∈S,存在着A1∈ 2A,使 B1=f (A1),由于f(A 1)={y|y∈B∧(x)(x ∈A1∧f (x)=y)}? B 所以 B1∈2B,故此S? 2B;又 B0=f (A)∈S ( 因为 A∈2A),所以 S非空;对于任何 B1,B2∈S,存在着 A1,A2∈2A,使得 B1=f (A1) , B2=f (A2) ,从而L∪B{B1,B2}=B 1∪B2=f (A1)f (A2) =f (A1∪A2) (习题三的8 的 1))由于 A1∪ A2? A,即 A1∪A2∈2A,因此 f (A1∪A2) ∈S,即上确界L∪B{B1,B2}存在。对于任何 B1,B2∈S,定义 A1=f – 1(B 1)={x|x∈A∧f (x) ∈B1}, A2=f-1(B 2)={x|x∈A∧ f (x)∈ B2} ,则 A1,A2∈ 2A,且显然 B1=f (A1) ,B2=f (A2) ,于是GLB{B1,B2}=B 1∩B2=f (A1) ∩f (A2)? f (A1∩A2) (习题三的8 的 2))又若 y∈B1∩B2,则 y∈B,且 y∈B2。由于 y∈ B1=f (A1)={y|y∈B∧(x)(x∈A1∧f (x)=y)},于是存在着x∈A1,使 f (x)=y,但是 f (x)=y∈B2。故此 x∈A2=f-1(B 2)={x|x∈A∧ f(x) ∈B2} ,因此 x∈A1∩A2,从而 y=f (x)∈ f (A1∩A2) ,所以GLB{B1,B2}=B 1∩B2=f (A1) ∩f (A2) ? f (A1∩A2)97313 这说明 GLB{B1,B2}=B 1∩B2=f (A1) ∩f (A2)=f (A1∩ A2) 于是从 A1∩A2∈2A可知 f (A1∩A2) ∈S,即下确界GLB{B1,B2} 存在。因此,〈S,? 〉是〈 2B,? 〉的子格。3.设〈 L,? 〉是格,任取a,b∈ L 且 a? b。证明〈 B, ? 〉是格。其中B={x|x ∈L 且 a? x? b}[ 证] 显然 B? L;根据自反性及a? b? b所以 a,b∈B,故此 B非空;对于任何 x,y∈B,则有 a? x? b 及 a? y? b,由于...