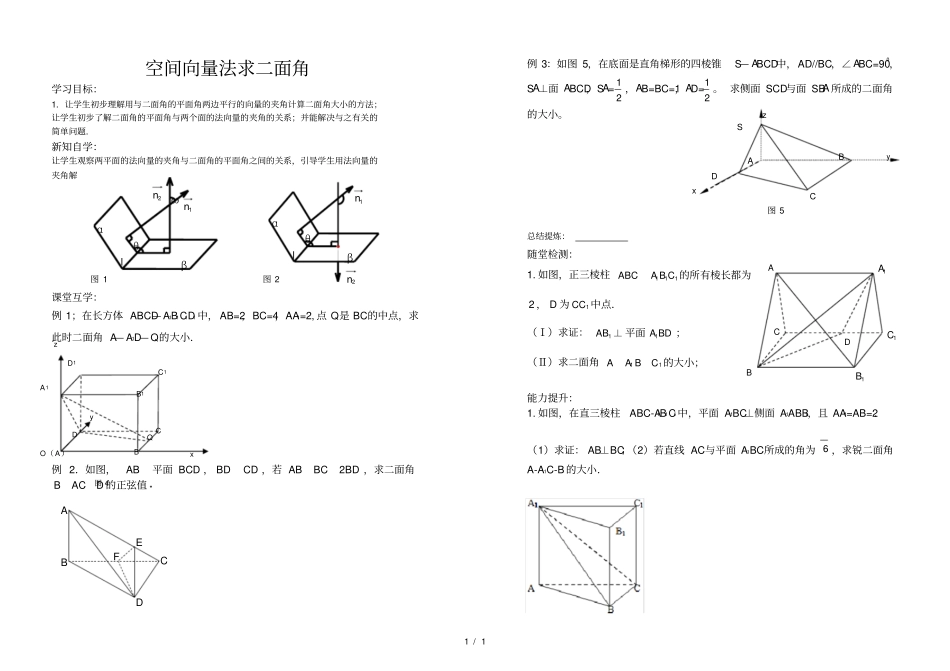
1 / 1 空间向量法求二面角学习目标:1.让学生初步理解用与二面角的平面角两边平行的向量的夹角计算二面角大小的方法;让学生初步了解二面角的平面角与两个面的法向量的夹角的关系;并能解决与之有关的简单问题.新知自学:让学生观察两平面的法向量的夹角与二面角的平面角之间的关系,引导学生用法向量的夹角解图 1 图 2课堂互学:例 1;在长方体 ABCD— A1B1C1D1 中, AB=2,BC=4,AA1=2, 点 Q是 BC的中点,求此时二面角 A— A1D— Q的大小.例 2.如图,AB平面 BCD , BDCD ,若2ABBCBD ,求二面角BACD 的正弦值例 3:如图 5,在底面是直角梯形的四棱锥S— ABCD中,AD//BC,∠ ABC=900,SA⊥面 ABCD,SA=21 ,AB=BC=1,AD=21 。 求侧面 SCD与面 SBA 所成的二面角的大小。总结提炼:随堂检测:1. 如图,正三棱柱111ABCA B C 的所有棱长都为2 , D 为1CC 中点.(Ⅰ)求证:1AB ⊥ 平面1A BD ;(Ⅱ)求二面角11CBAA的大小;能力提升:1. 如图,在直三棱柱ABC-A1B1C1中,平面 A1BC⊥侧面 A1ABB1,且 AA1=AB=2.(1)求证: AB⊥BC;(2)若直线 AC与平面 A1BC所成的角为 6 ,求锐二面角A-A1C-B 的大小.ABCDEFωθβlα2n1nθβlα1n2nO( A )B A1C1B1D1D C Q z y x 图 4 A z y x D C B S 图 5 A B C D 1A1C1B