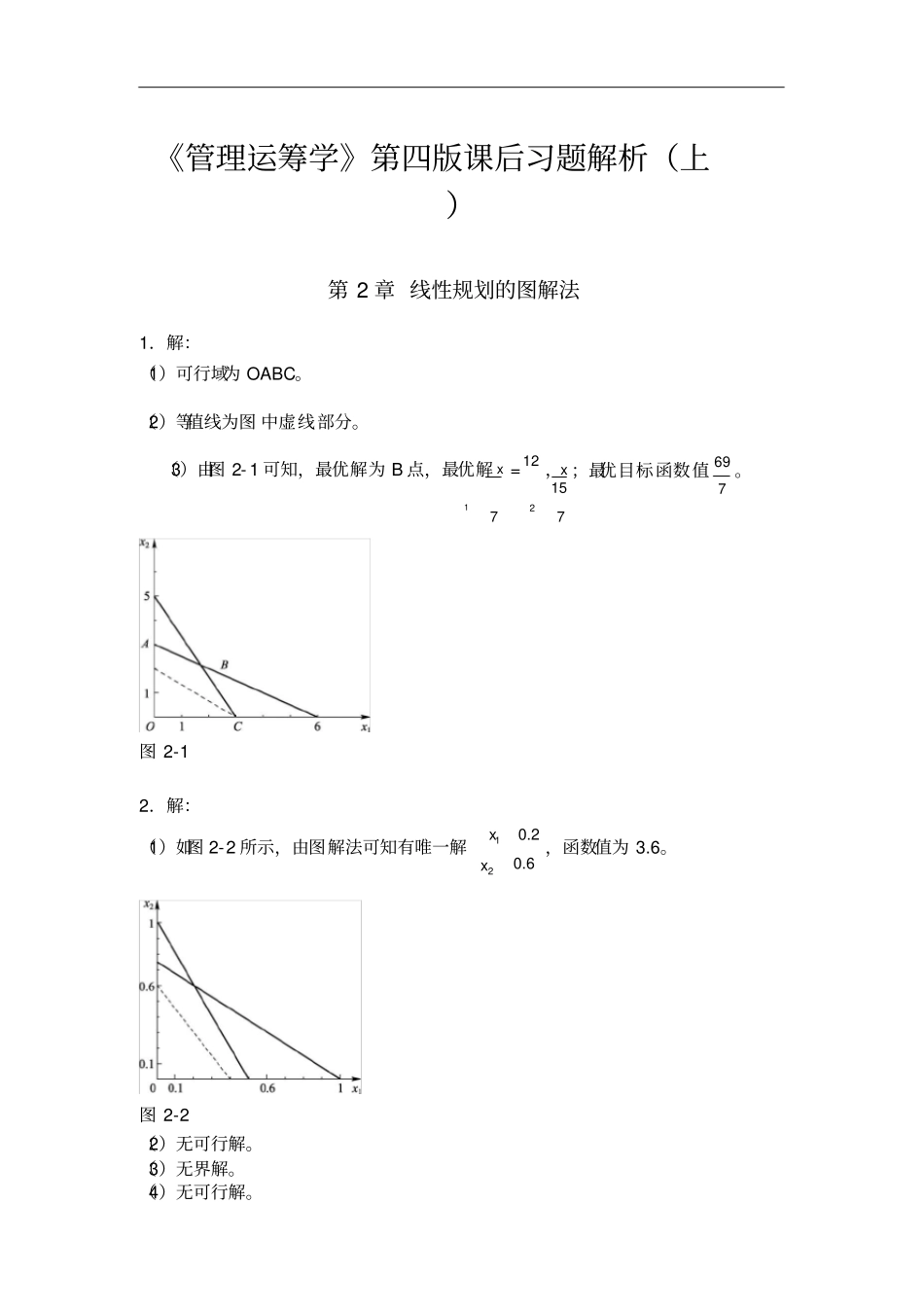
0.6 《管理运筹学》第四版课后习题解析(上)第 2 章 线性规划的图解法1.解:(1)可行域为 OABC。(2)等值线为图 中虚线部分。(3)由图 2- 1 可知,最优解为 B 点,最优解 x = 12 ,x 151 7 2 7图 2-1;最优目标函数值 69 。7 2.解:(1)如图 2-2 所示,由图解法可知有唯一解x1 0.2 ,函数值为 3.6。x2 图 2-2(2)无可行解。(3)无界解。(4)无可行解。(5)无穷多解。x (6)有唯一解120 3 ,函数值为 92 。8 3 x 2 3 3.解:(1)标准形式max f 3x1 2x2 0s1 0s2 0s39x1 2x2 s1 30 3x1 2x2 s2 13 2x1 2x2 s3 9 x1, x2 , s1, s2 , s3 ≥ 0 (2)标准形式min f 4 x1 6x2 0s1 0s23x1 x2 s1 6 x1 2x2 s2 10 7x1 6x2 4 x1, x2 , s1, s2 ≥ 0 (3)标准形式min f x12 x22 x20s1 0s23x1 5x25x2s1 70 2x15x25x250 3x12x22x2s2 30 x1, x2 , x2, s1, s2 ≥ 0 4.解:标准形式max z 10 x1 5 x2 0s1 0s23x1 4x2 s1 9 5x1 2x2 s2 8 x1, x2 , s1, s2 ≥ 0 ≤松弛 变量(0,0)最优解为 x1 =1,x2=3/2。5.解:标准形式min f 11x1 8 x2 0s1 0s2 0s310x1 2x2 s1 20 3x1 3x2 s2 18 4x1 9x2 s3 36 x1, x2 , s1, s2 , s3 ≥ 0 剩余 变量(0, 0, 13)最优解为 x1=1,x2=5。6.解:(1)最优解为 x1=3,x2=7。(2)1 c1 3 。(3)2 c2 6 。(4)x1 6。x2 4。(5)最优解为 x1=8,x2=0。(6)不变化。因为当斜率1≤c1c21 ,最优解不变,变化后斜率 为 1,所以最优解 3 不变。7. 解:设 x,y 分别为甲、乙两种柜的日 产量,目标函数 z=200x+240y, 线性约束条件:解6x 12 y 1208x 4 y 64 即x 0 y 0 x 2 y 202x y 16 x 0 y 0 作出可行域.x 2 y 202x y 16 得Q(4,8)z 最大200 4 240 8 2720 答:该公司安排甲、乙两种柜的日 产量分 别为 4 台和 8 台,可获最大利 润 2720 元.8.解:设需截第一种 钢板 x 张,第二种钢板 y 张,所用钢板面 积zm2.目标函数 z=x+2y,线性约束条件:x y 122x y 15 x 3y 27 x 0 y 0 x 3y 27作出可行域,并做一 组一组平行直 线 x+2y=t .解x y 12 得 E(9 / 2,15 / 2)3x+2y,线性约束条件2x y 3.但 E不是可行域内的整点,在可行域的整点中,点(4...